Задание № 1319 
Классификатор алгебры: 6.7. Тригонометрические уравнения на формулы суммы или разности аргументов
Задания на 10 баллов
i
Найдите сумму корней уравнения
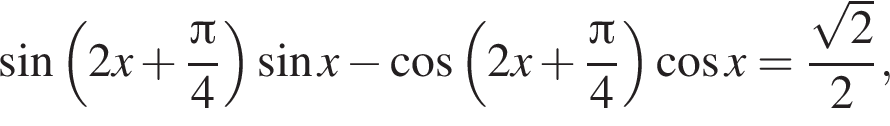
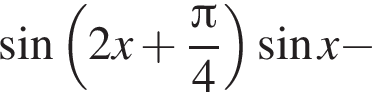
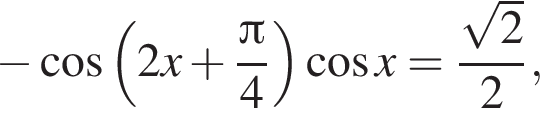
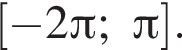
Решение. Воспользовавшись формулой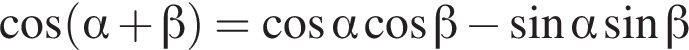 
последовательно получаем:
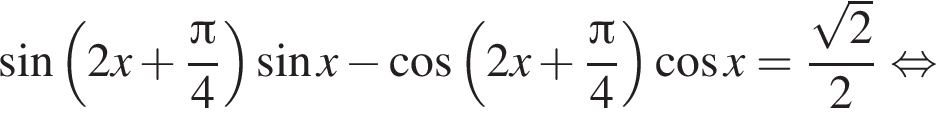
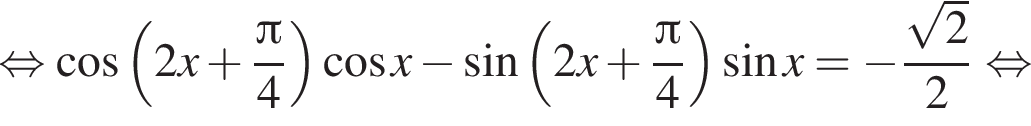
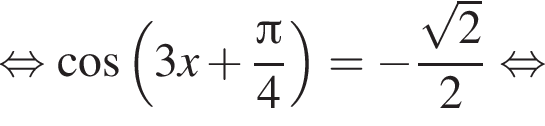
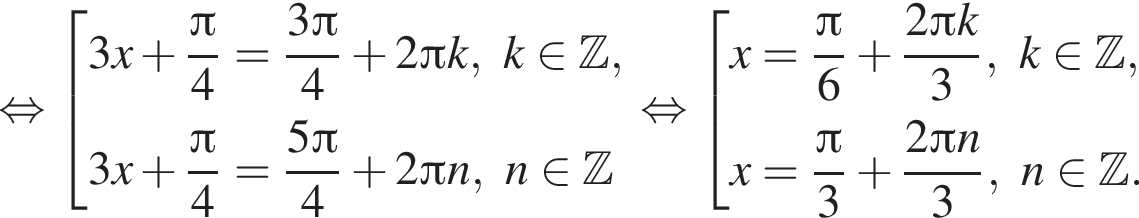
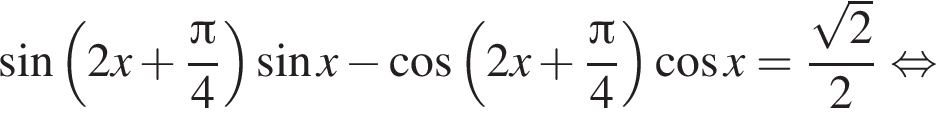
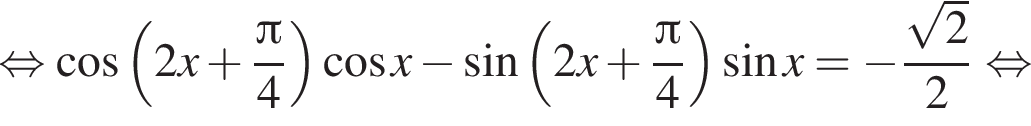
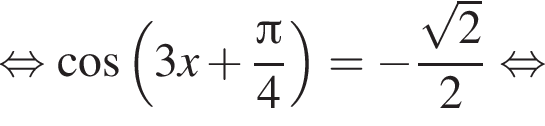
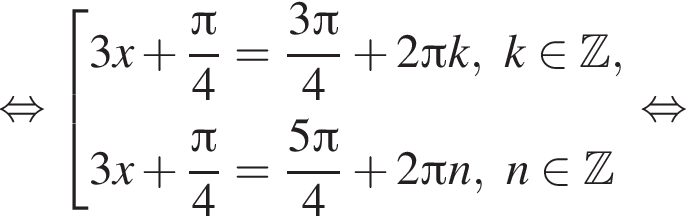
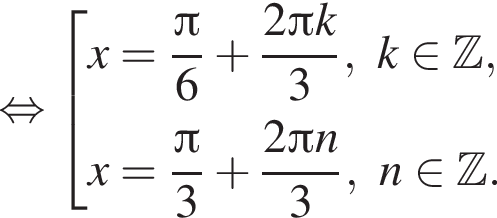
Найдем значения k, при которых корни уравнения принадлежат промежутку 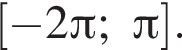Имеем:
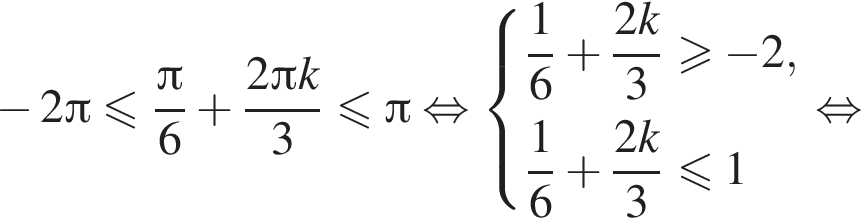
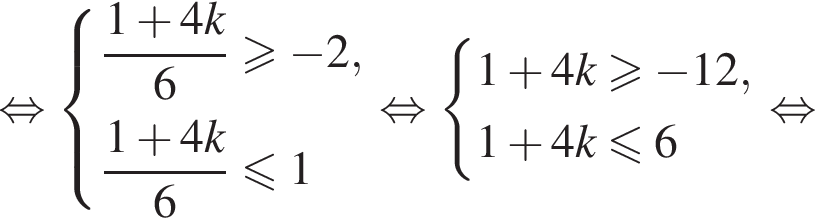
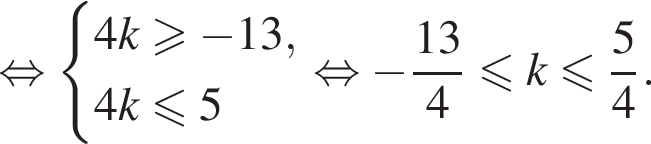
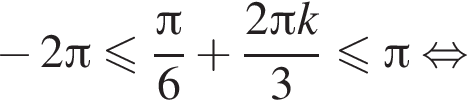
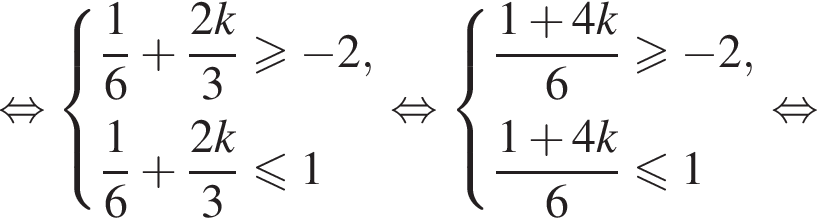
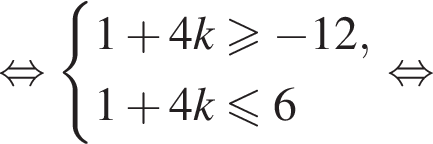
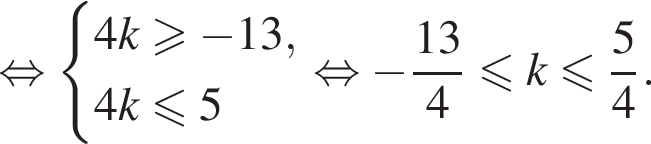
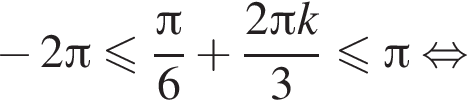
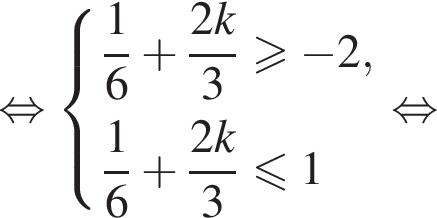
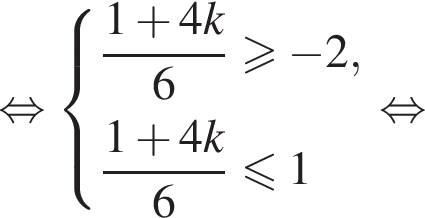
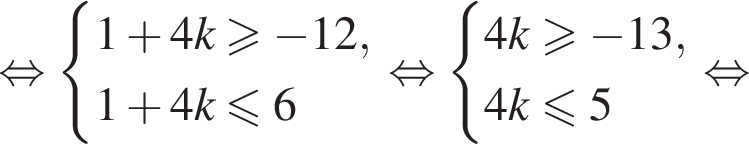
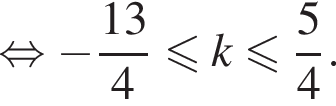
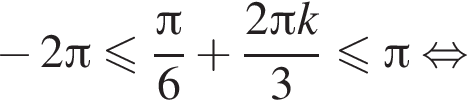
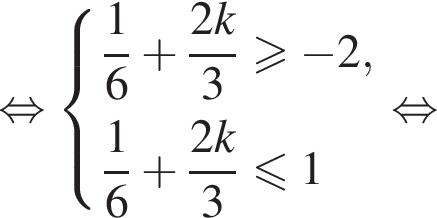
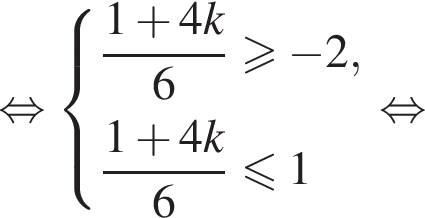
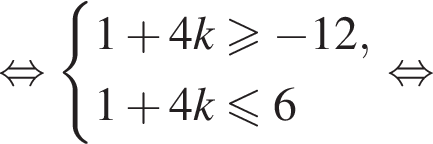
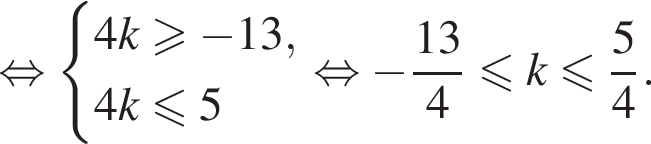
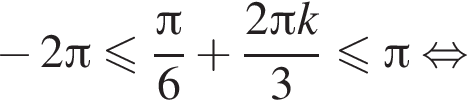
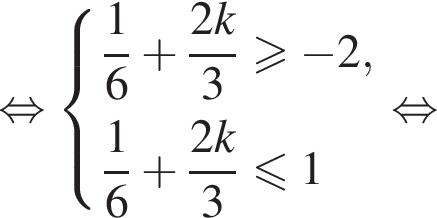
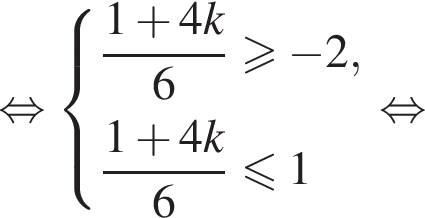
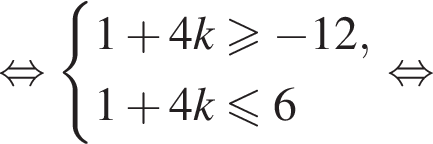
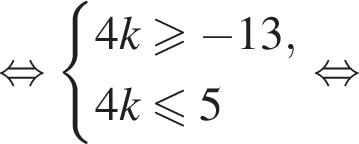
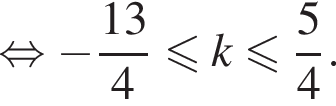
Так как k является целым числом, решениями неравенства являются числа −3, −2, −1, 0, 1. Найдем корни уравнения при данных значениях k:
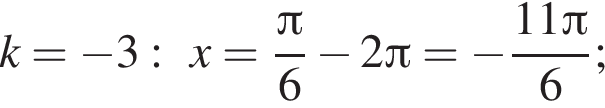
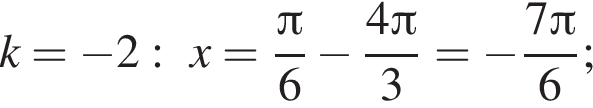
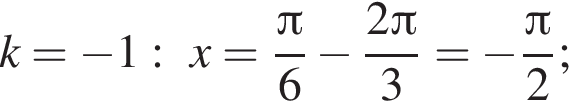
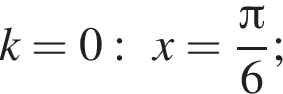
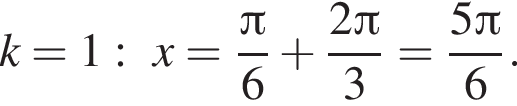
Найдем значения n, при которых корни уравнения принадлежат промежутку 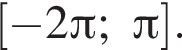Имеем:
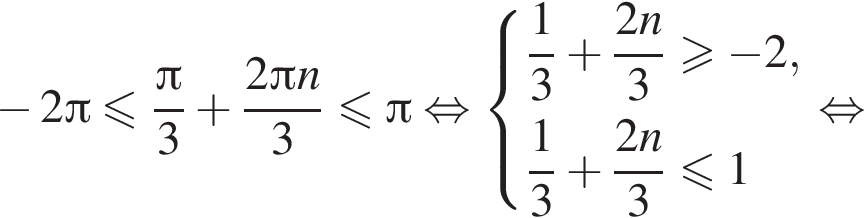
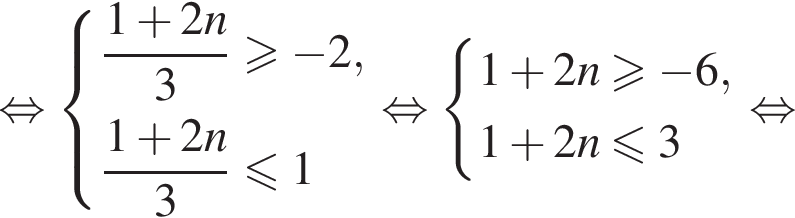
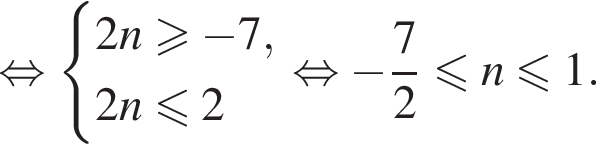
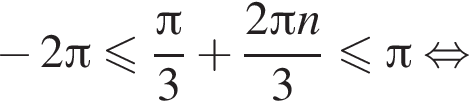
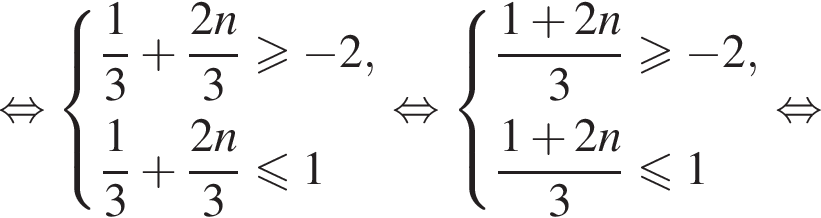
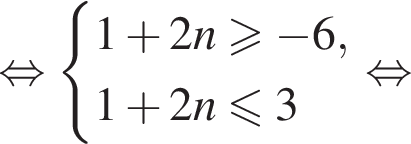
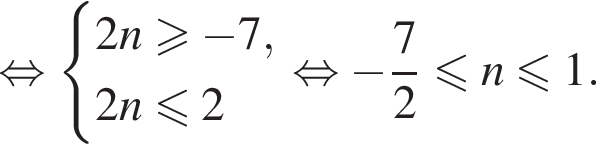
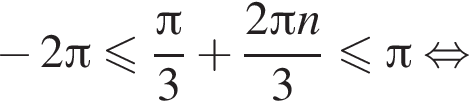
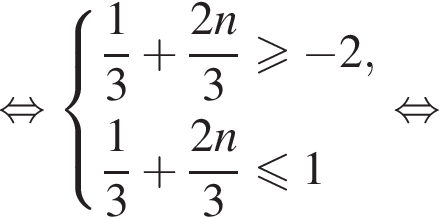
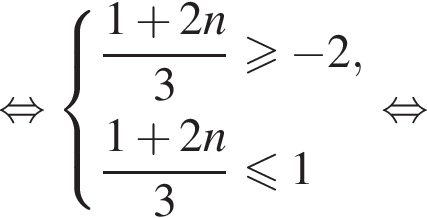
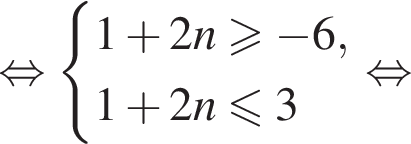
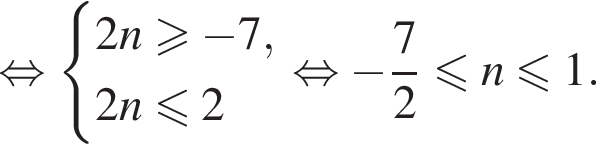
Так как n является целым числом, решениями неравенства являются числа −3, −2, −1, 0, 1. Найдем корни уравнения при данных значениях n:
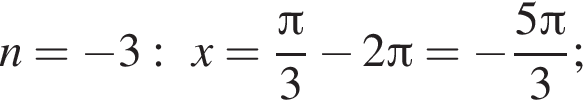
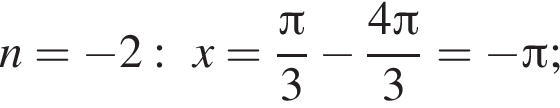
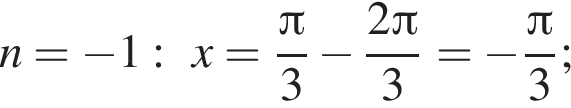
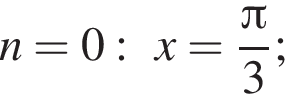
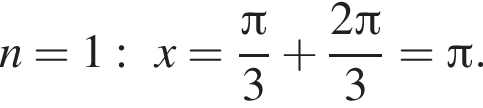
Найдем сумму всех корней уравнения, принадлежащий промежутку 
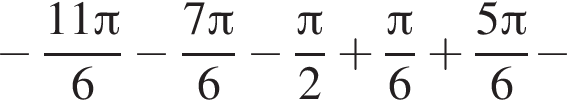
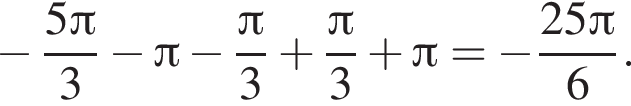
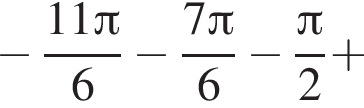
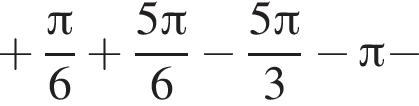
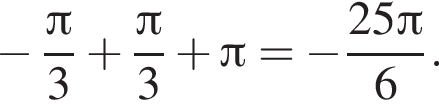
Ответ: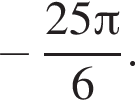 
Ответ: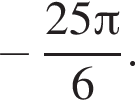
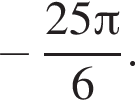
1319
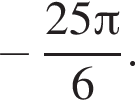
Классификатор алгебры: 6.7. Тригонометрические уравнения на формулы суммы или разности аргументов