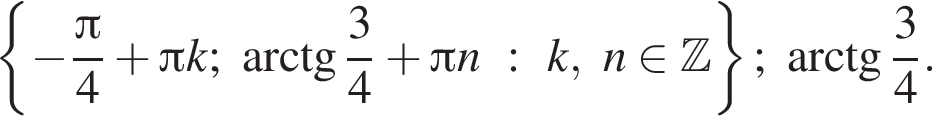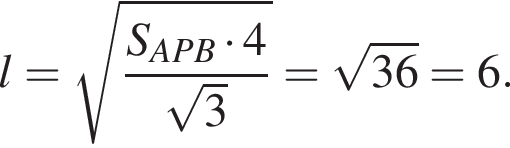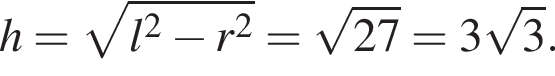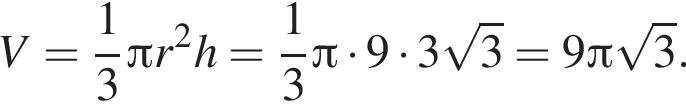1. Задание № 481 

Классификатор алгебры: 1.7. Преобразование буквенных логарифмических выражений, 1.13. Справедливость алгебраических утверждений
Задания на 1 балл
i
Укажите формулу логарифма произведения:
а)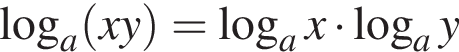
б)
в)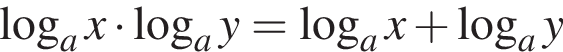
г)
Решение. Формула логарифма произведения:
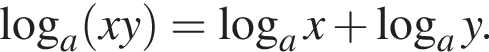
Ответ: б.
Ответ: б.
481
б
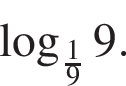
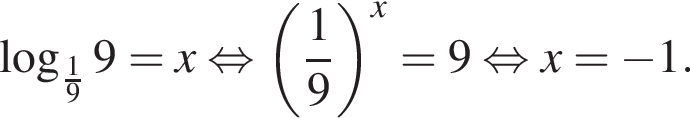
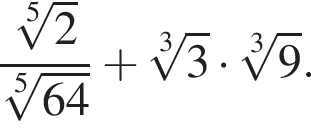
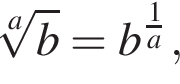 а затем вычислим
а затем вычислим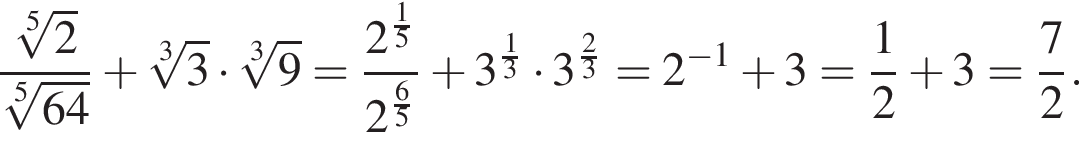
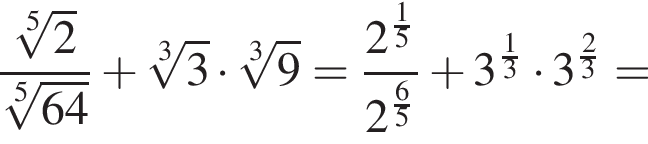
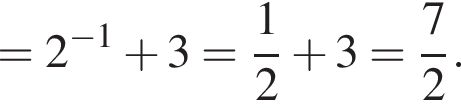
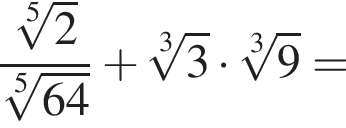
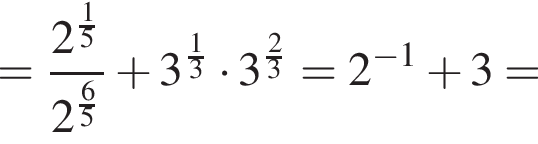
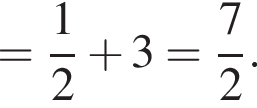
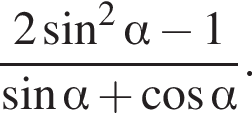
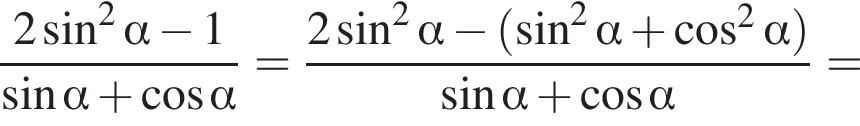
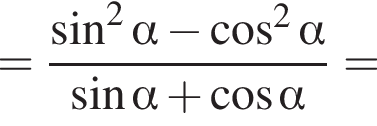
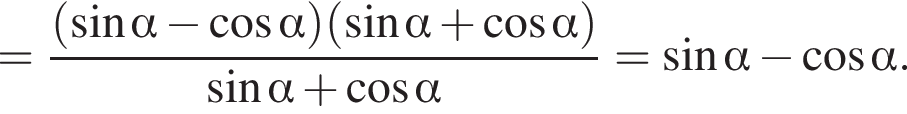
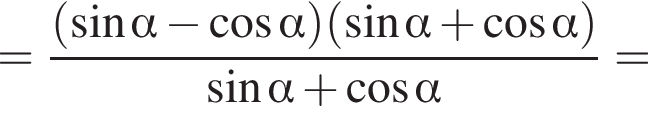

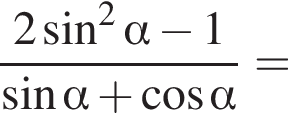
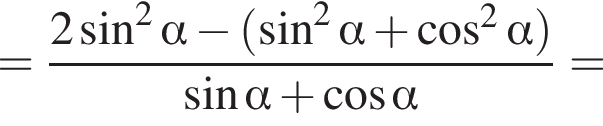

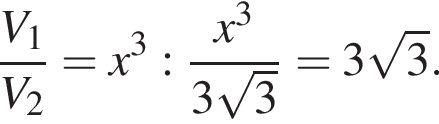
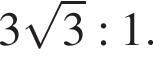
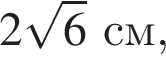 и углом 30°.
и углом 30°. Отрезок CO — высота конуса, отрезок OB — радиус. Зная угол, найдем OC и OB:
Отрезок CO — высота конуса, отрезок OB — радиус. Зная угол, найдем OC и OB: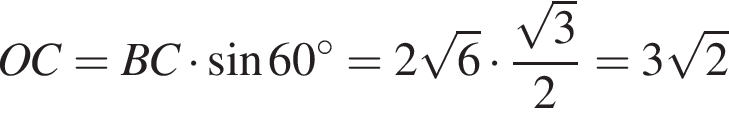 см
см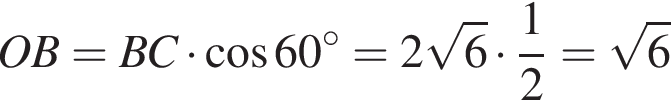 см
см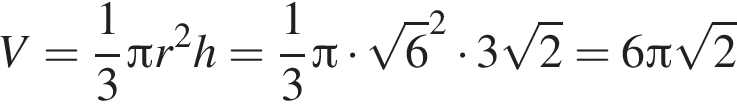 см3.
см3.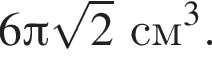
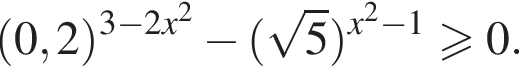

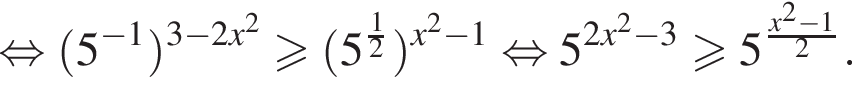
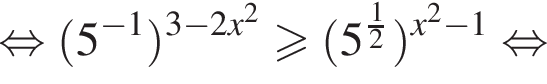
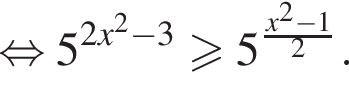
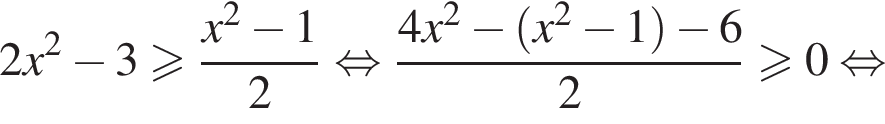
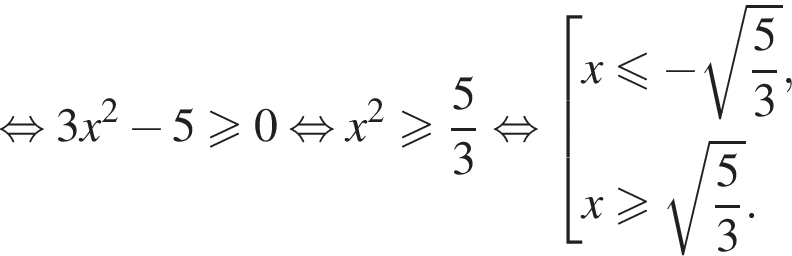
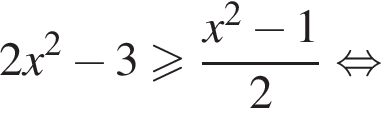
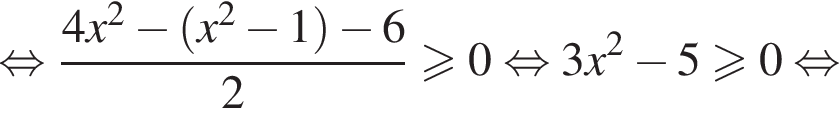
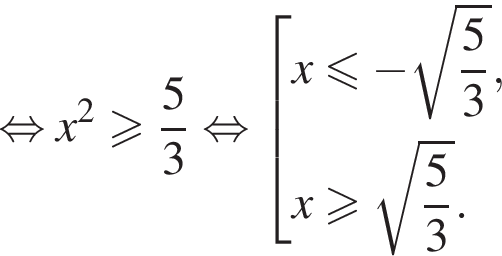
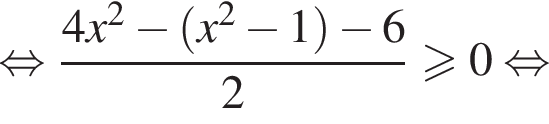
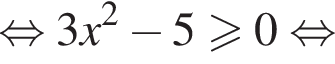
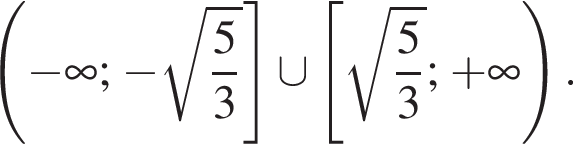
 и укажите какое-нибудь его решение, удовлетворяющее неравенству
и укажите какое-нибудь его решение, удовлетворяющее неравенству 

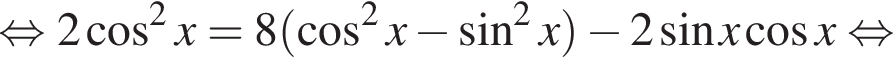
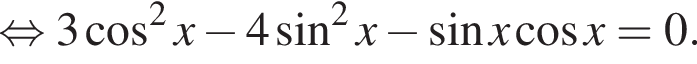
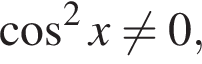 если cos2x = 0, то sin2x = 1, что противоречит условию, тогда разделим на cos2x. Имеем:
если cos2x = 0, то sin2x = 1, что противоречит условию, тогда разделим на cos2x. Имеем: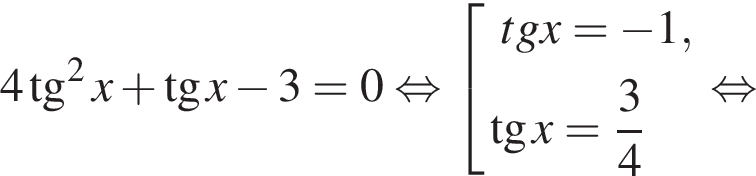
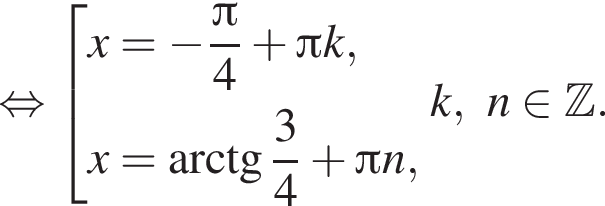
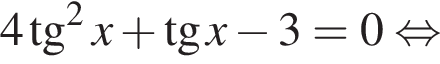
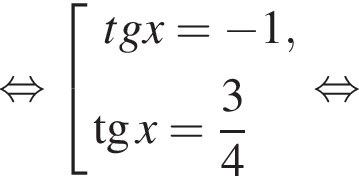
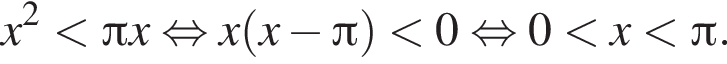
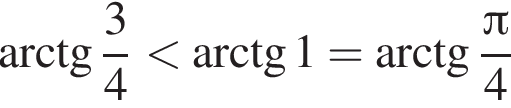 удовлетворяет данному неравенству.
удовлетворяет данному неравенству.