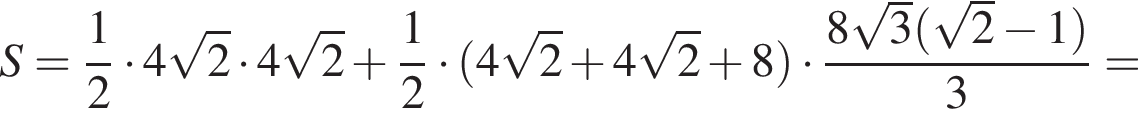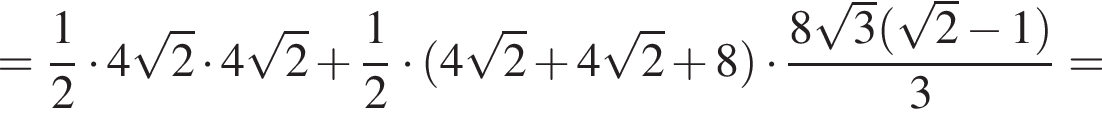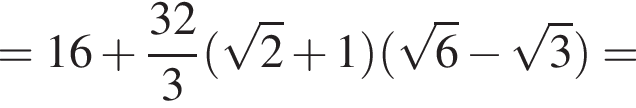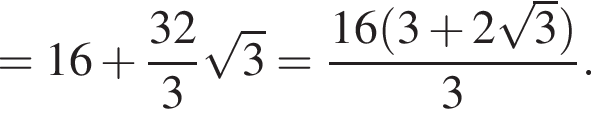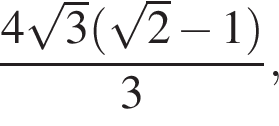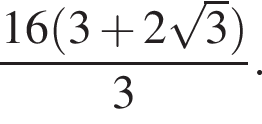i
В основании пирамиды лежит равнобедренный треугольник с углом при вершине 90° и большей стороной 8 см, все двугранные углы при ребрах основания равны по 30°. Найдите высоту и площадь полной поверхности пирамиды.

 Площадь треугольника равна половине произведения его катетов, либо произведению радиуса вписанной окружности на полупериметр, в нашем случае
Площадь треугольника равна половине произведения его катетов, либо произведению радиуса вписанной окружности на полупериметр, в нашем случае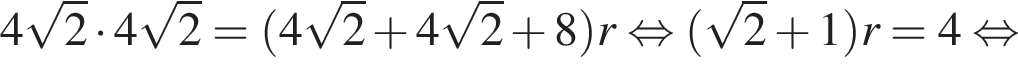
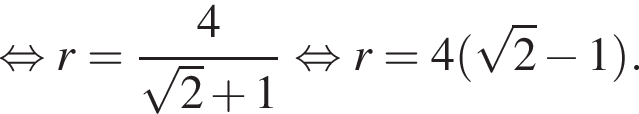
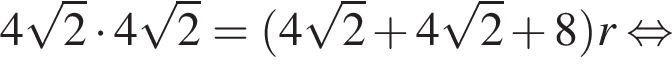
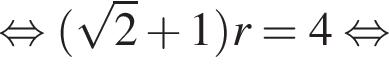
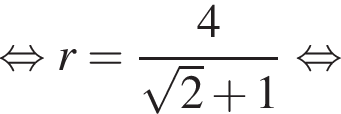

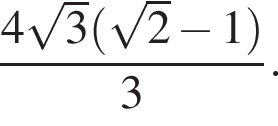 Гипотенуза DK — апофема пирамиды — равна частному от деления OK на косинус угла при боковой стороне, то есть
Гипотенуза DK — апофема пирамиды — равна частному от деления OK на косинус угла при боковой стороне, то есть 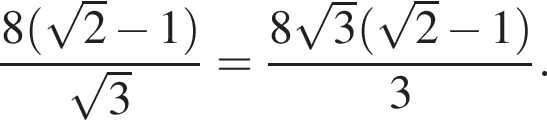 Площадь полной поверхности пирамиды равна сумме площадей боковой поверхности и основания, где площадь боковой поверхности равна половине произведения периметра основания на апофему. Имеем
Площадь полной поверхности пирамиды равна сумме площадей боковой поверхности и основания, где площадь боковой поверхности равна половине произведения периметра основания на апофему. Имеем