Задание № 656 
Классификатор алгебры: 3.2. Правильная треугольная пирамида, 4.2. Объем многогранника, 5.4. Другие задачи на построение сечений, 5.9. Периметр, площадь сечения
Методы алгебры: Теорема Пифагора
Задания на 6 баллов
i
Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4 м, а плоский угол при вершине пирамиды равен 60°.
Решение. Основанием правильной четырехугольной пирамиды — квадрат, боковые грани — равнобедренные треугольники. Рассмотрим треугольник DSC — равнобедренный. По условию
тогда 
Тогда треугольник DSC равносторонний, значит,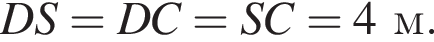 
Проведем высоту SO. Точка O — центр окружности, описанной вокруг основания. Найдем радиус окружности:
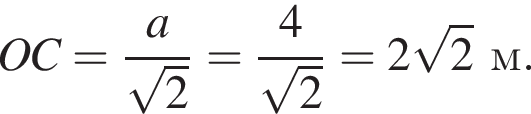
По теореме Пифагора из треугольника COS:
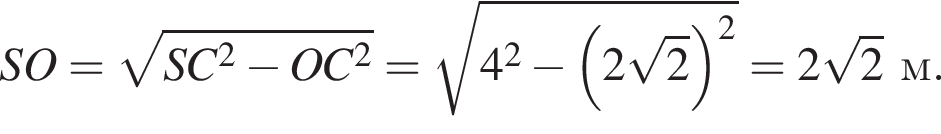
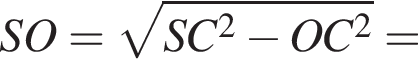
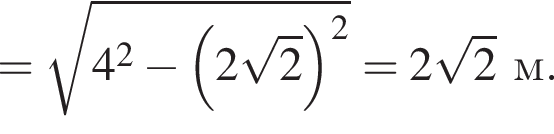
Воспользуемся формулой объема пирамиды:
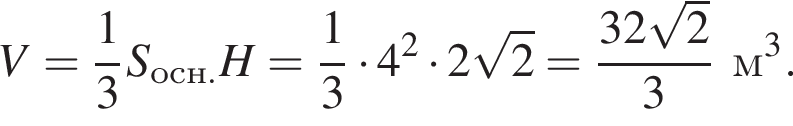
Ответ: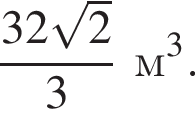 
Ответ: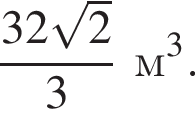
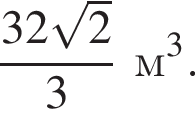
656
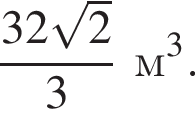
Классификатор алгебры: 3.2. Правильная треугольная пирамида, 4.2. Объем многогранника, 5.4. Другие задачи на построение сечений, 5.9. Периметр, площадь сечения
Методы алгебры: Теорема Пифагора