Дана правильная треугольная пирамида PABC, у которой боковое ребро равно 7, ребро основания — 6; точка M — середина ребра PC. Постройте сечение пирамиды плоскостью, проходящей через точки A и M параллельно ребру PB и найдите длину наибольшей стороны этого сечения.
РЕШУ ЦТ — математика–11Б
Варианты заданий
1.
i
2.
i
Дана правильная треугольная пирамида PABC, у которой боковое ребро равно 14, ребро основания — 8; точка M — середина ребра PB. Постройте сечение пирамиды плоскостью, проходящей через точки A и M параллельно ребру PC и найдите длину наименьшей стороны этого сечения.

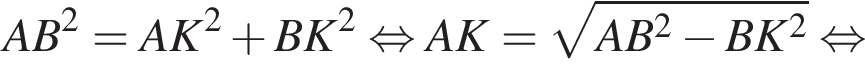
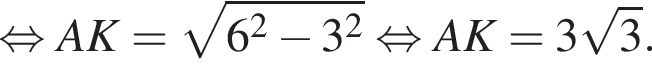
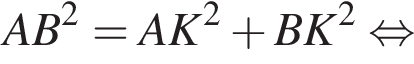


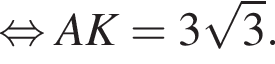
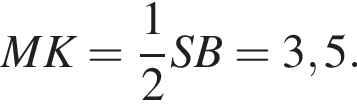 Применим теорему косинусов в треугольнике ASC:
Применим теорему косинусов в треугольнике ASC: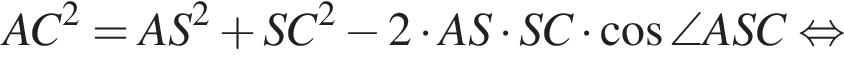
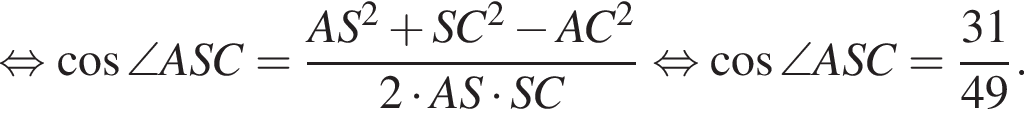
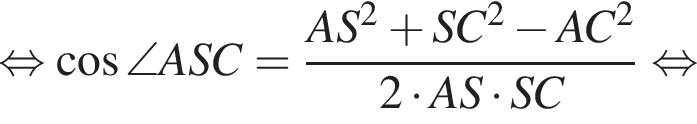
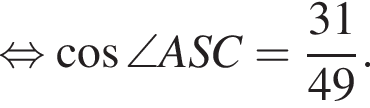
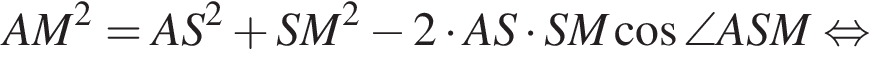
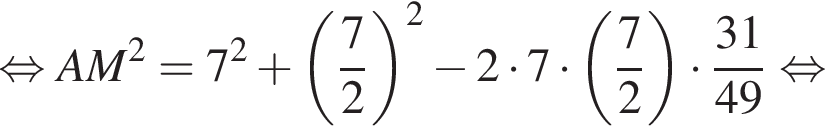
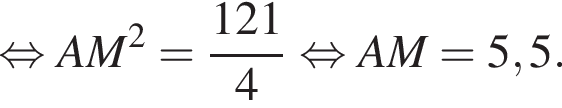
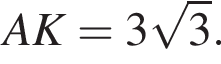 Наибольшей стороной является сторона AM, ее длина равна 5,5.
Наибольшей стороной является сторона AM, ее длина равна 5,5.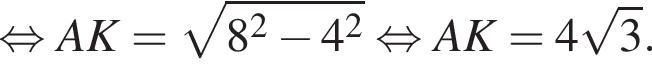
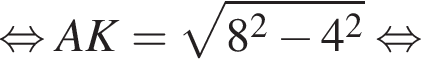
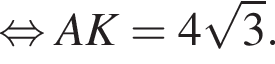
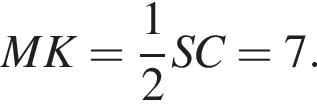 Применим теорему косинусов в треугольнике ABS:
Применим теорему косинусов в треугольнике ABS: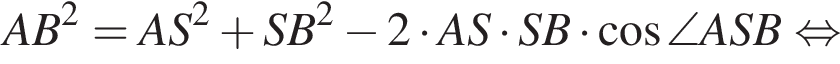
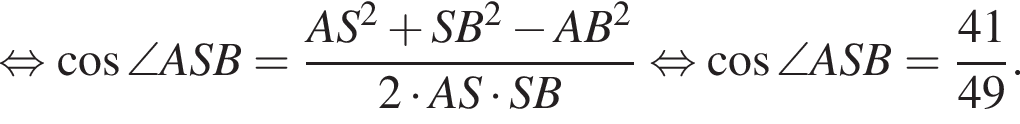
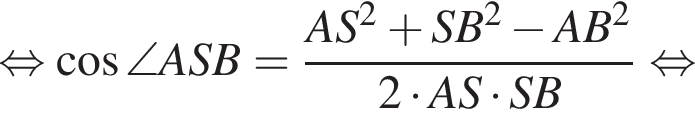
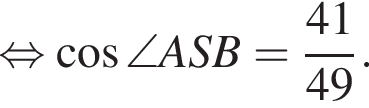
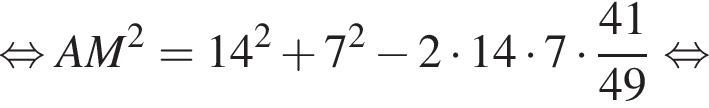
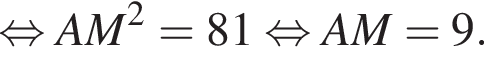
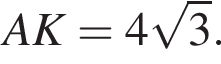 Наименьшей стороной является сторона AK, ее длина равна
Наименьшей стороной является сторона AK, ее длина равна