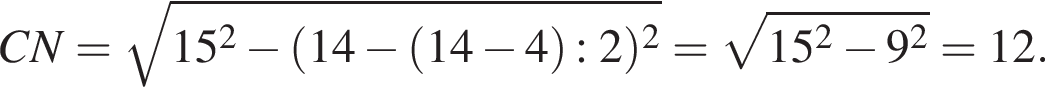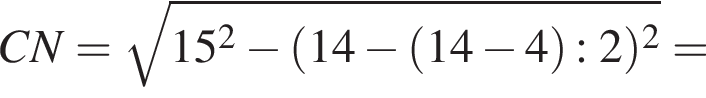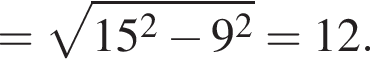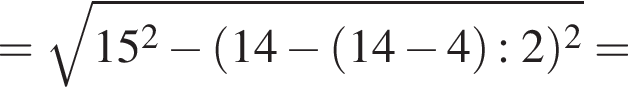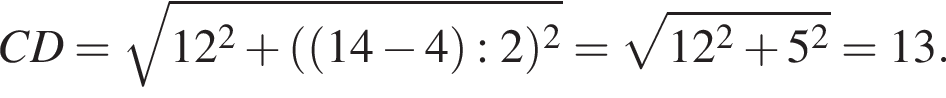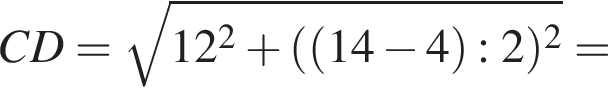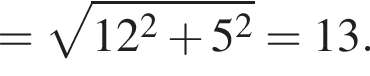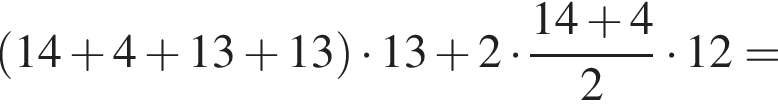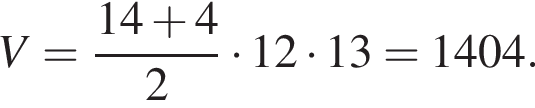Укажите рисунок, на котором изображен график функции y = ![]() :
:
На рисунке изображен куб MNKPM1N1K1P1. Четырехугольник NN1P1P1 является:
а) квадратом
б) ромбом с острым углом при вершине P
в) трапецией
г) прямоугольником ( ).
).
Вычислите: 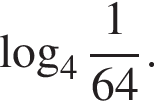
Решите уравнение: 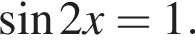
Решите неравенство 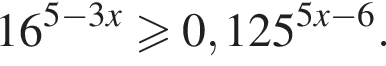
Диагональ основания правильной четырехугольной пирамиды равна 8 см, угол между плоскостями боковой грани и основания равен 45°. Найдите площадь полной поверхности пирамиды.
Решите неравенство: 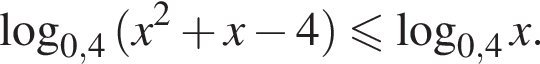
Упростите выражение 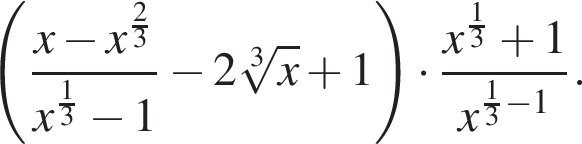
Решите уравнение  и укажите какое-нибудь его решение, удовлетворяющее неравенству
и укажите какое-нибудь его решение, удовлетворяющее неравенству 
Основанием прямой призмы является равнобедренная трапеция с основаниями 4 и 14 см и диагональю 15 см. Две боковые грани призмы — квадраты. Найдите площадь поверхности и объем призмы.

 изображён на рисунке б).
изображён на рисунке б).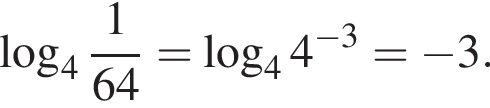
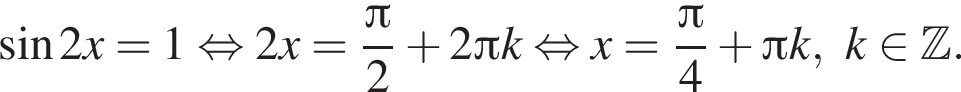
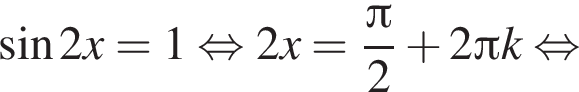
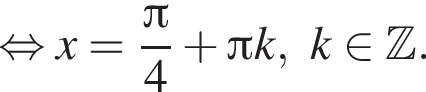
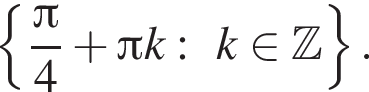
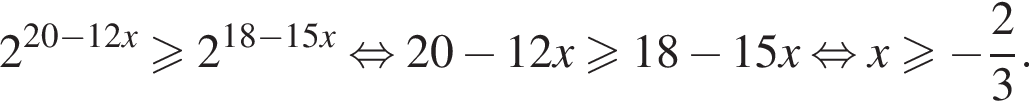
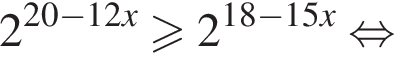
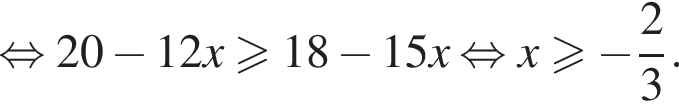

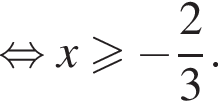
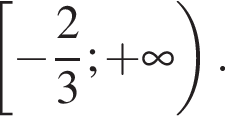
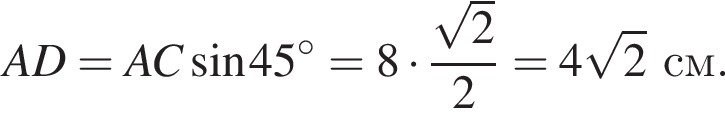
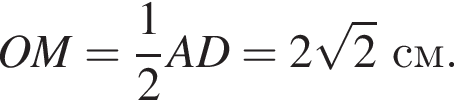 В треугольнике SOM имеем:
В треугольнике SOM имеем: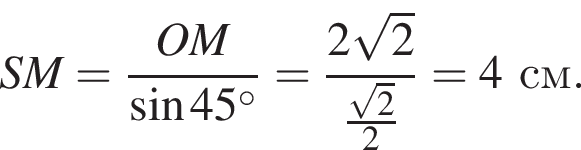
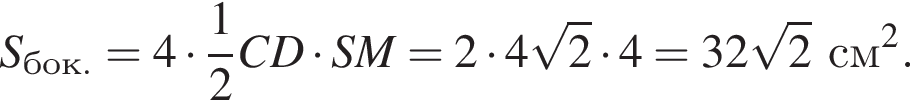
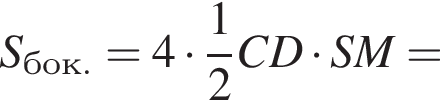
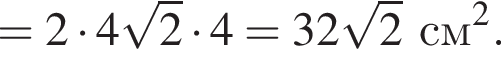
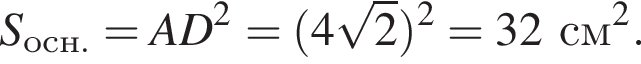
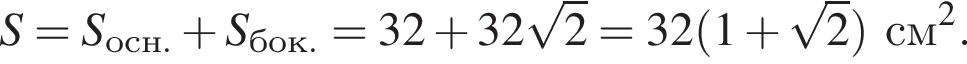

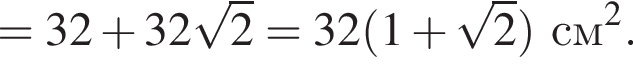
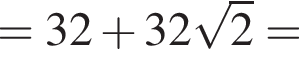
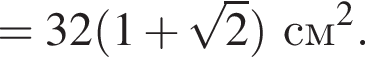

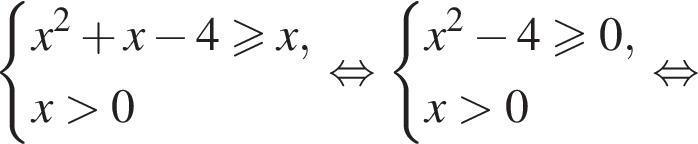
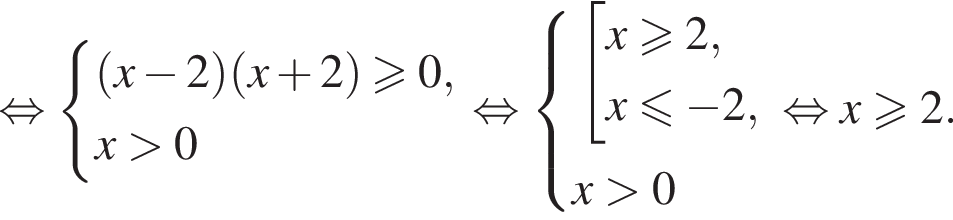
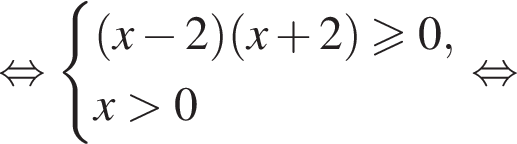
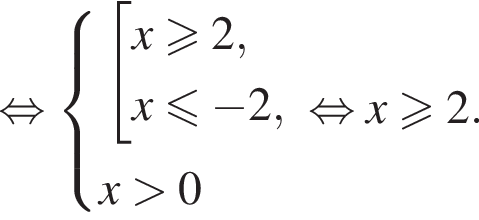
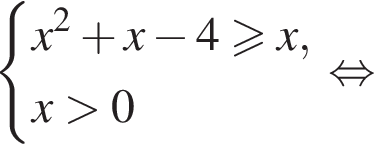
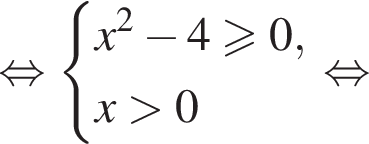

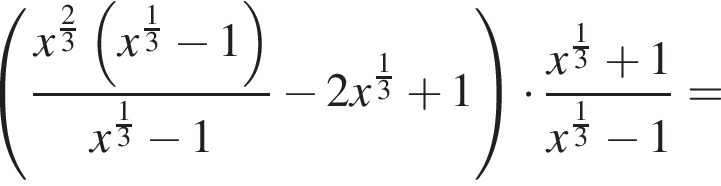
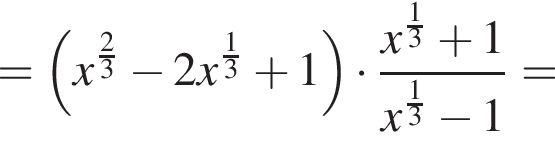
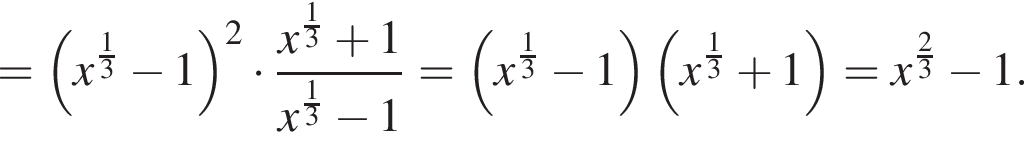
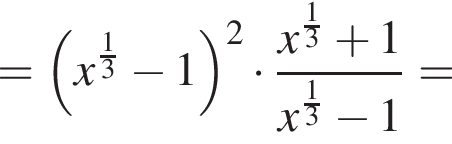
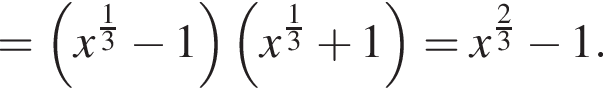
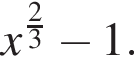

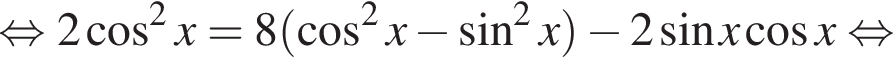
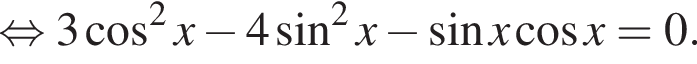
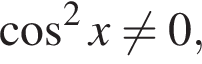 если cos2x = 0, то sin2x = 1, что противоречит условию, тогда разделим на cos2x. Имеем:
если cos2x = 0, то sin2x = 1, что противоречит условию, тогда разделим на cos2x. Имеем: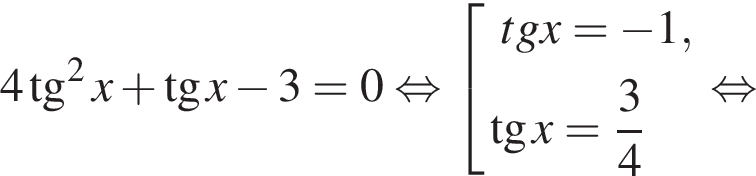
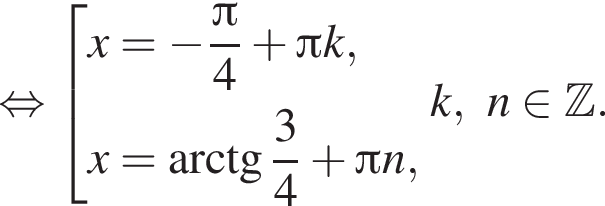
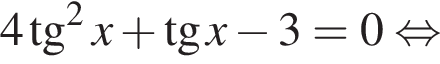
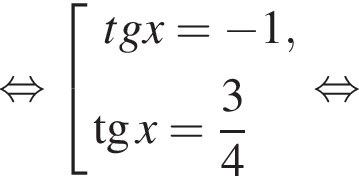
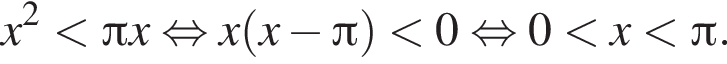
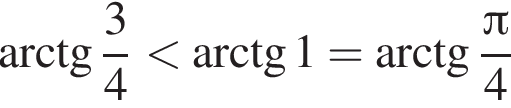 удовлетворяет данному неравенству.
удовлетворяет данному неравенству.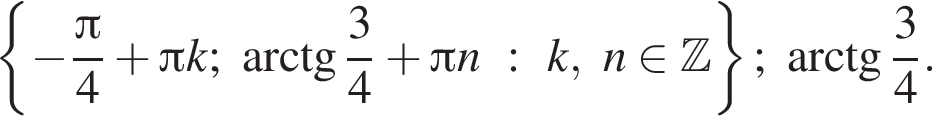
 в нашем случае, AN = AD − (AD − BC) : 2, то есть
в нашем случае, AN = AD − (AD − BC) : 2, то есть