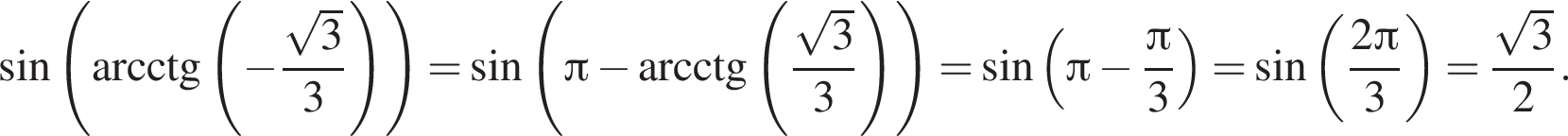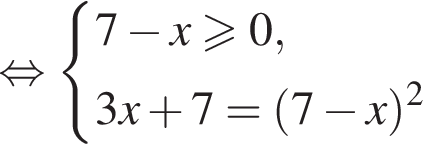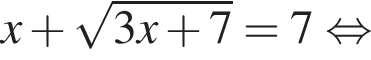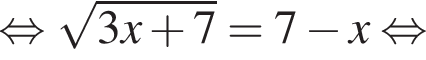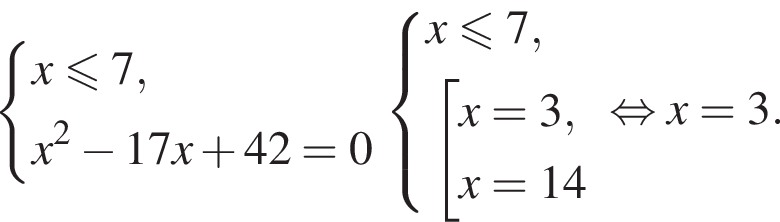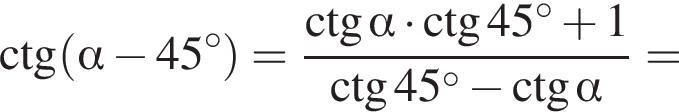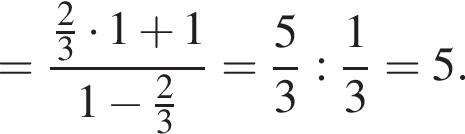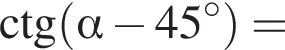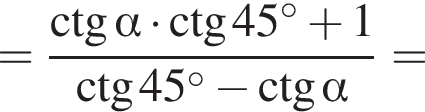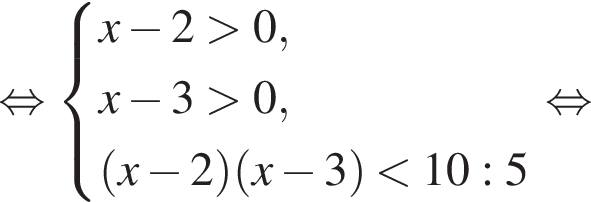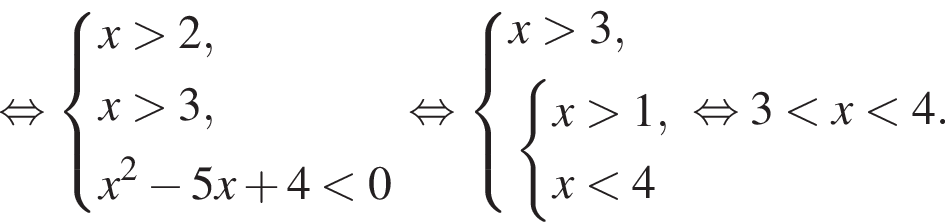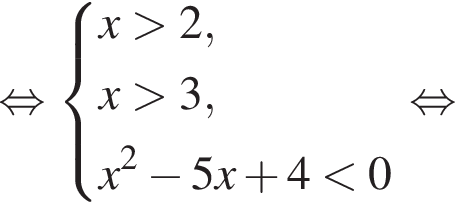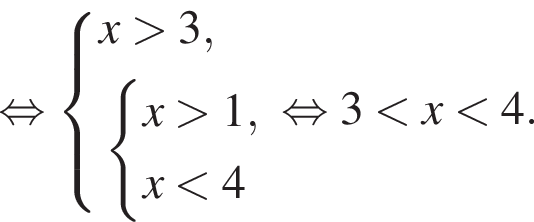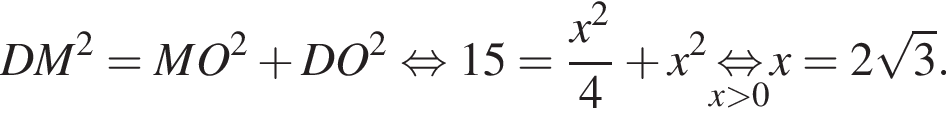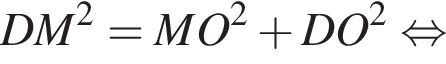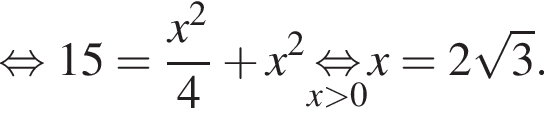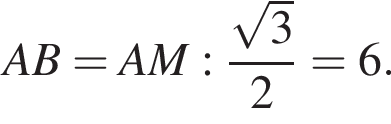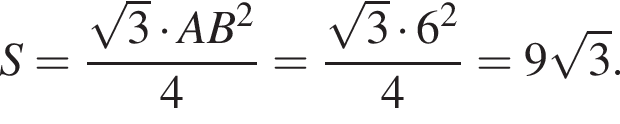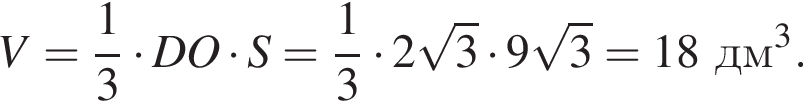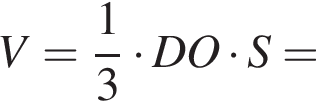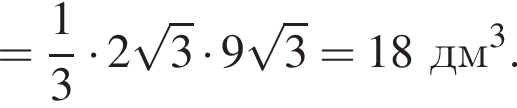Укажите рисунок, на котором изображен график функции 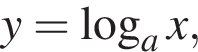 где
где ![]() :
:
Укажите верное утверждение.
Конус может быть получен вращением:
а) прямоугольника вокруг одной из его сторон
б) параллелограмма вокруг одной из его сторон
в) прямоугольной трапеции вокруг меньшего основания
г) прямоугольного треугольника вокруг одного из катетов
Вычислите: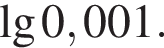
Представьте в виде степени с основанием a выражение 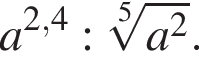
Решите уравнение 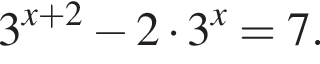
На рисунке изображена развертка правильной треугольной призмы. Используя данные рисунка, найдите площадь полной поверхности призмы.
Вычислите: 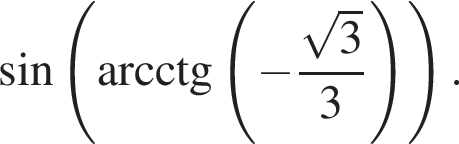
Решите уравнение: 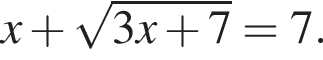
Решите неравенство: 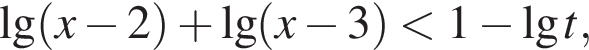 где
где 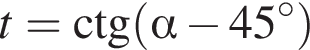 и
и 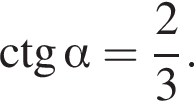
Найдите объем правильной треугольной пирамиды, если ее боковое ребро наклонено к плоскости основания под углом 45°, а апофема равна ![]() дм.
дм.

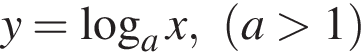 изображён на рисунке б).
изображён на рисунке б).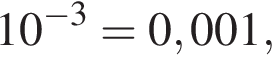 получаем, что
получаем, что 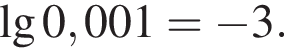
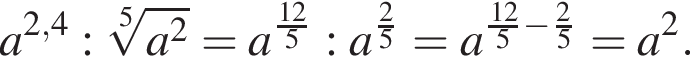
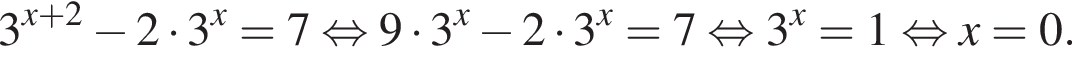
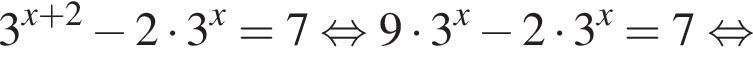
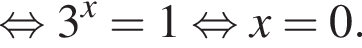
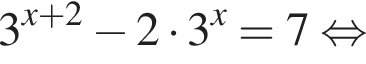
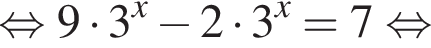
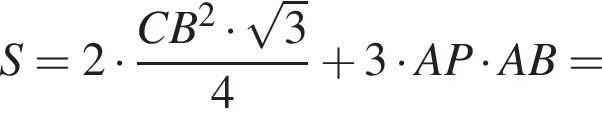
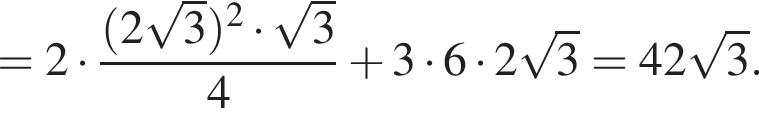
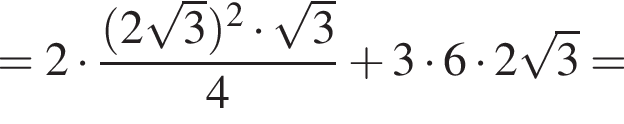
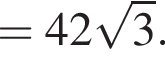
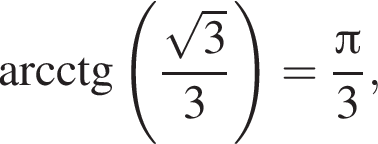 вычислим значение исходного выражения:
вычислим значение исходного выражения: