1.
i
Укажите результат внесения множителя под знак корня в выражении 
:
а) 
б) 
в) 
г) 
РЕШУ ЦТ — математика–11Б
Вариант № 23
2.
i
Укажите прямоугольник, при вращении которого вокруг одной из сторон может быть получен цилиндр с радиусом основания, равным 3 см, и образующей, равной 5 см:
3.
i
Найдите шестой член бесконечно убывающей геометрической прогрессии: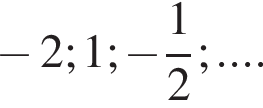 
а первый элемент равен −2. Так как 
тогда:
4.
i
Решите уравнение: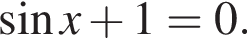 
5.
i
Найдите значение выражения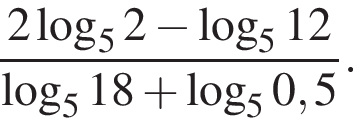 
6.
i
В правильной треугольной усеченной пирамиде стороны оснований равны 6 и 3 см. Высота усеченной пирамиды равна 
Найдите площадь боковой поверхности усеченной пирамиды.
B
Тогда подставим и получим, что 
а 
Точки O и O1 — центры треугольников ABC и A1B1C1 соответственно, тогда 
а 
В прямоугольной трапеции HH1O1O проведем H1K — высоту, причем H1K = O1O. Найдём KH: KH = OH − KO = OH − H1O1. Подставим и получим, что 
Из треугольника HKH1 найдём HH1 по теореме Пифагора: 
Подставим и получим, что площадь боковой поверхности равна 27.7.
i
Решите уравнение: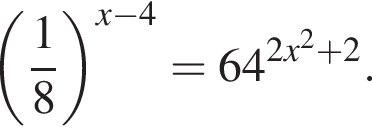 
8.
i
Найдите наибольшее целое значение x, удовлетворяющее неравенству: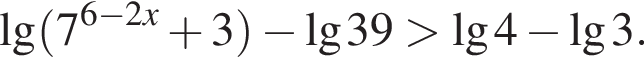 
9.
i
Решите уравнение: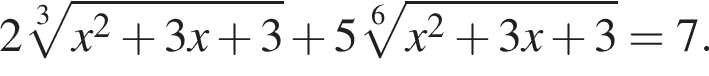 
тогда:
10.
i
Угол между плоскостями 
и 
равен 30°. Точка B находится на расстоянии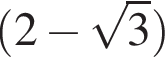 
см от плоскости и 2 см от плоскости 
Найдите расстояние от точки B до прямой пересечения плоскостей и
Подставим и получим, что 
Вокруг четырёхугольника ABCD можно описать окружность, так как суммы противоположных углов равны 180°. Из треугольника CBD найдём радиус этой окружности по теореме синусов: 
Поскольку угол ACB — прямой, то он опирается на диаметр, то есть 
