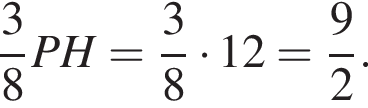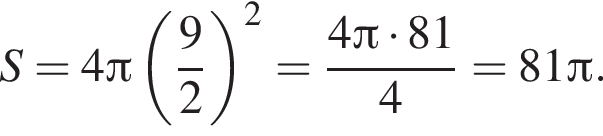Укажите рисунок, на котором изображена графическая иллюстрация системы уравнений 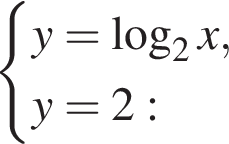
РЕШУ ЦТ — математика–11Б
Вариант № 2554
1.
i
2.
i
Диаметр сферы равен ![]() см, тогда радиус ограниченного этой сферой шара равен:
см, тогда радиус ограниченного этой сферой шара равен:
а) ![]() см
см
б) ![]() см
см
в) ![]() см
см
г) ![]() см
см
3.
i
Найдите значение выражения : ![]()
4.
i
Решите уравнение: 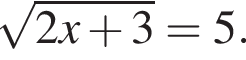
5.
i
Решите уравнение: 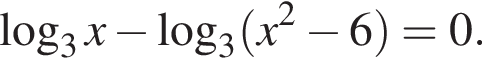
6.
i
Дан куб ABCDA1B1C1D1 с ребром, равным 30 см. Постройте сечение куба плоскостью, проходящей через ребро AA1 и середину ребра BC. Найдите периметр сечения.
7.
i
Найдите область определения выражения : 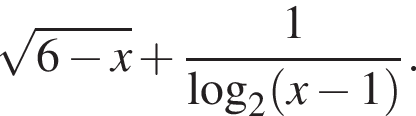
8.
i
Решите уравнение: 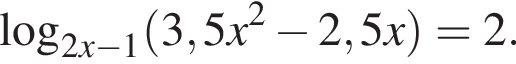
9.
i
Найдите наименьшее целое решение неравенства: 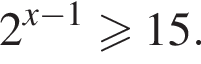
10.
i
В правильную четырехугольную пирамиду вписана сфера, центр которой делит высоту пирамиды в отношении ![]() считая от вершины. Найдите площадь сферы, если сторона основания пирамиды равна 18.
считая от вершины. Найдите площадь сферы, если сторона основания пирамиды равна 18.

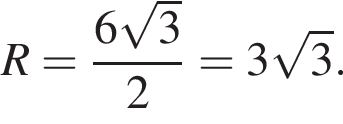
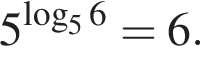
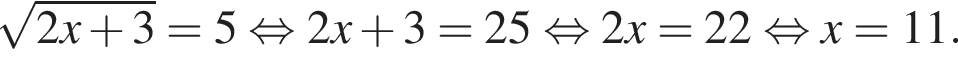
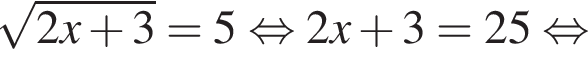
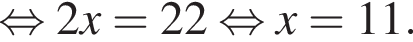
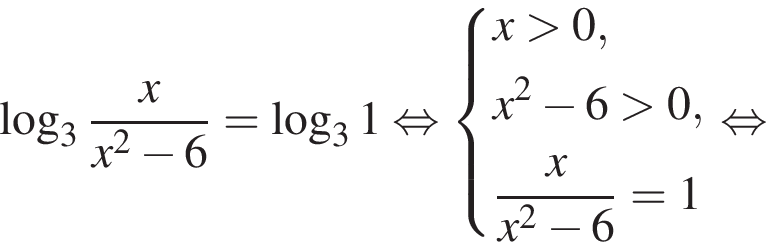
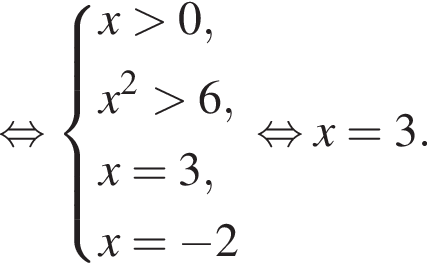
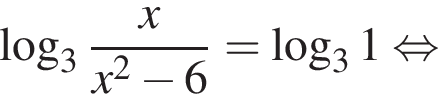
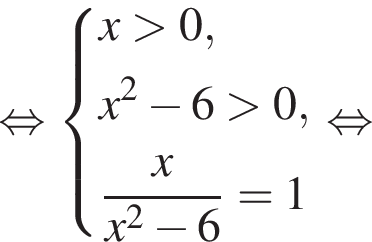
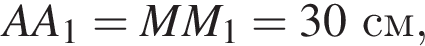
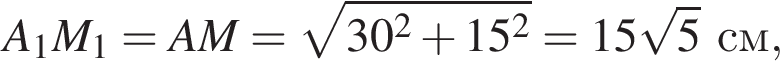

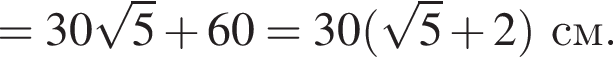

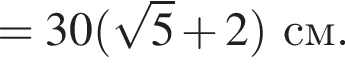
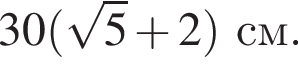
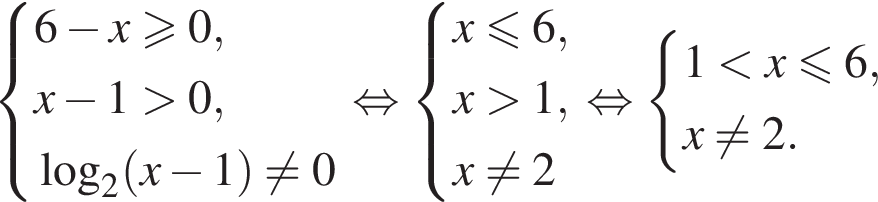
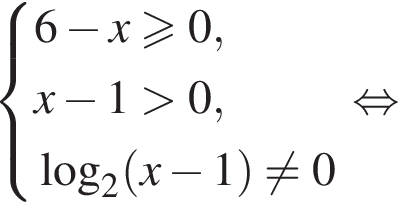
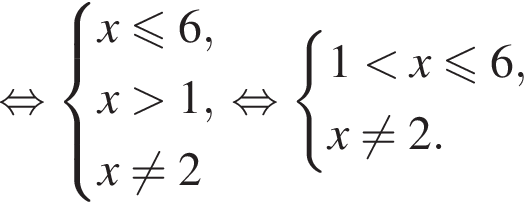

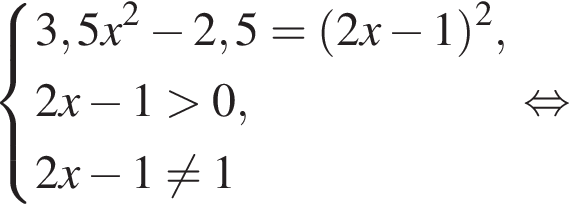
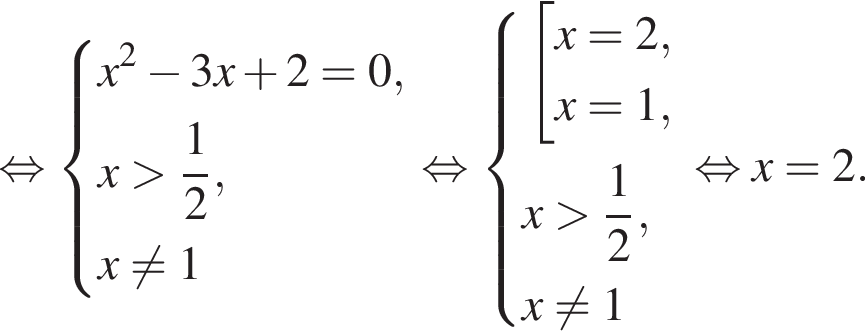
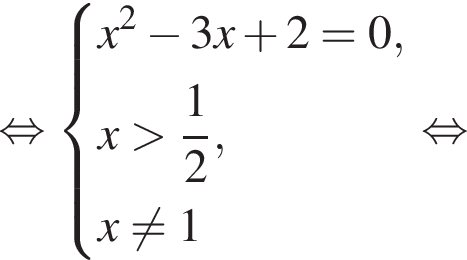
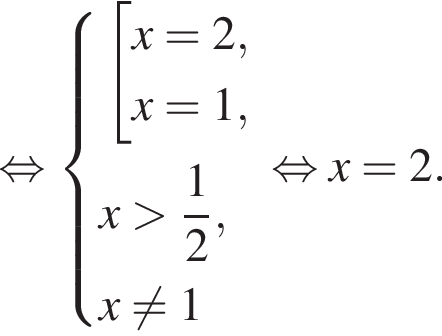

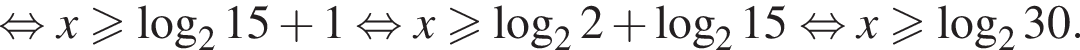
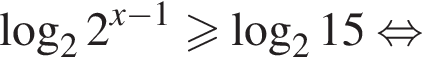

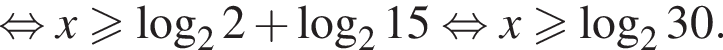
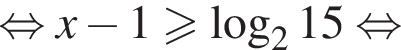
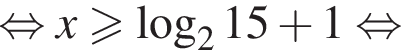
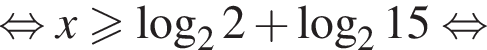
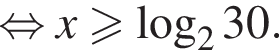
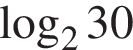 больше 4 и меньше 5, поэтому наименьшее целое решение данного неравенства — число 5.
больше 4 и меньше 5, поэтому наименьшее целое решение данного неравенства — число 5.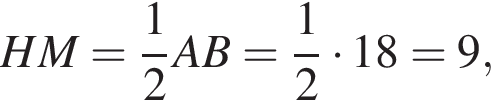
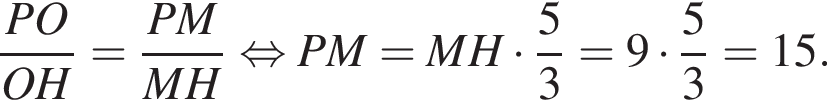
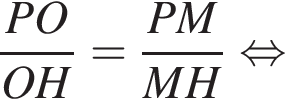
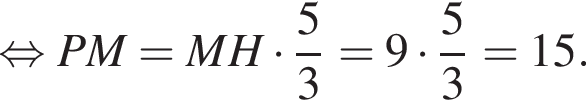
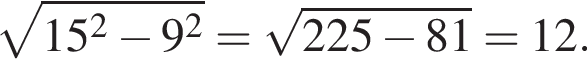 Радиус сферы, равный OH,
Радиус сферы, равный OH,