1.
i
Разверткой боковой поверхности цилиндра является:
a) круг;
в) прямоугольник;
б) трапеция;
r) треугольник.
РЕШУ ЦТ — математика–11Б
Вариант № 3872
2.
i
Укажите рисунок, на котором изображен график функции y = 
:
изображён на рисунке б).3.
i
Укажите верное равенство:
а)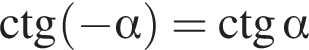 
б)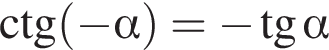 
в) 
г)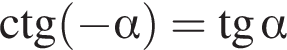 
4.
i
Укажите рисунок, на котором изображена графическая иллюстрация системы уравнений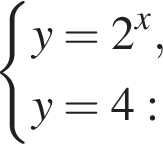 
5.
i
Выразите в радианах угол 45°:
а) 
б) 
в) 
г) 
рад, то 
рад.6.
i
Если 2x = 7, то:
а) 
б)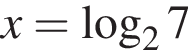 
в)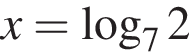 
г) 
Значит, правильный ответ под буквой б).7.
i
Диаметр сферы равен 
см, тогда радиус ограниченного этой сферой шара равен:
а) 
см
б) 
см
в) 
см
г) 
см
8.
i
Укажите рисунок, на котором изображена графическая иллюстрация системы уравнений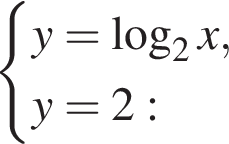 
9.
i
Степенная функция задана формулой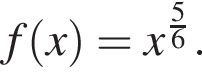 
Выберите верное равенство:
а)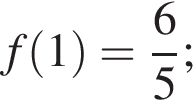 
б)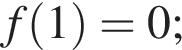 
в)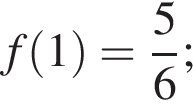 
г)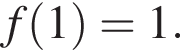 
10.
i
Производная функции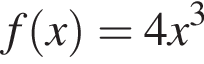 
равна:
а) 
б) 
в) 
г) 
11.
i
Определите верное равенство:
a)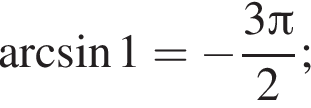 
б)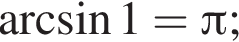 
в)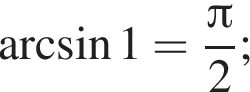 
г)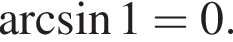 
называют такое число из отрезка 
синус которого равен 
Иными словами, 
— решение уравнения 
где 
Решим уравнение: 
На данном промежутке отберём корни и получим, что 
Поэтому правильный ответ в).12.
i
Укажите верные равенства:
а)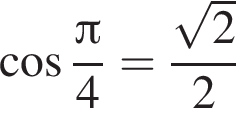 
б)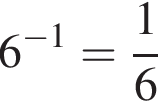 
в)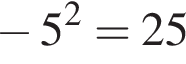 
г)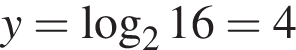 
поэтому второе равенство верно. Третье равенство неверно в виду отсутствия скобок, то есть в квадрат возводится число 5, а после этого его знак меняется на противоположный. Так как 
— это решение уравнения 
четвёртое равенство верно. 13.
i
Выберите рисунок, на котором изображена графическая модель системы уравнений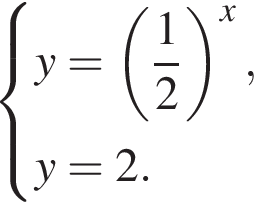 
— показательная функция. Она определена при всех x и убывает.
—14.
i
Укажите функции, графики которых проходят через точку (0;0):
а) 
б) 
в)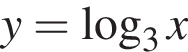 
г) 
15.
i
Определите, какое наименышее количество граней может иметь призма:
a) 3;
б) 4;
в) 5;
г) 6.
16.
i
На рисунке изображен график функции:
а)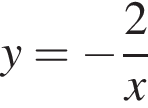 
б) 
в)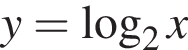 
г) 
17.
i
Укажите верное равенство :
а)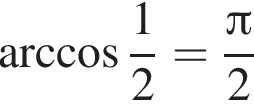 
б)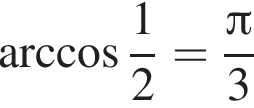 
в)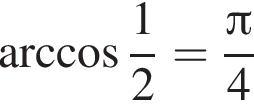 
г)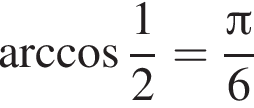 
называют такое число из отрезка 
косинус которого равен 
— решение уравнения 
где 
Решим уравнение: 
Найдём корень на промежутке 
Тогда 
Поэтому правильный ответ б).18.
i
Логарифмическая функция задана формулой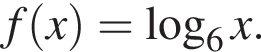 
Выберите верное равенство:
а)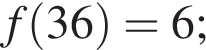 
б)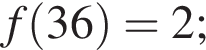 
в)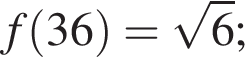 
г)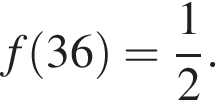 
19.
i
Если 3x = 5, то:
а)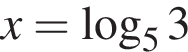 
б) 
в)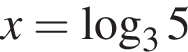 
г) 
Значит, правильный ответ под буквой в).20.
i
Знаменателем бесконечно убывающей геометрической прогрессии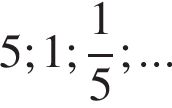 
является число:
а) 
б) 
в) 
г) 
Правильный ответ находится под буквой г).