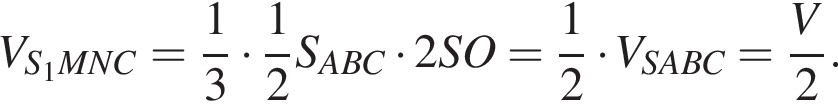1. Задание № 601 

Классификатор алгебры: 1.6. Вычисление логарифмов, 1.13. Справедливость алгебраических утверждений
Задания на 1 балл
i
Укажите верное равенство:
а) 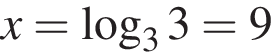
б) 
в) 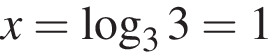
г) 
Решение. Так как 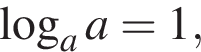 то
то 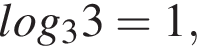 а значит, правильный ответ в).
а значит, правильный ответ в).
Ответ: в).
Ответ: в).
601
в
Классификатор алгебры: 1.6. Вычисление логарифмов, 1.13. Справедливость алгебраических утверждений
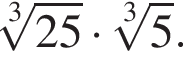
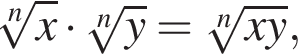 то имеем:
то имеем:
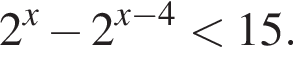
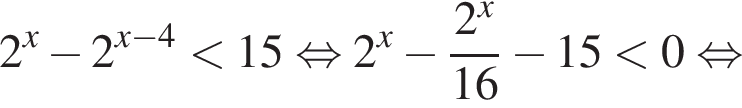
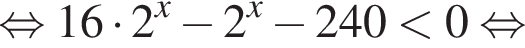

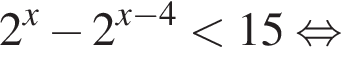
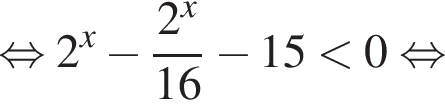
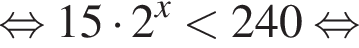
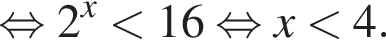
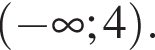
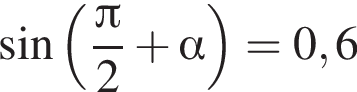 и
и 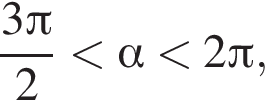 то
то 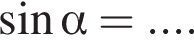
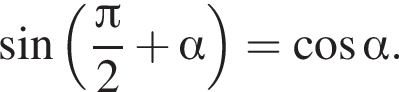 Так как
Так как 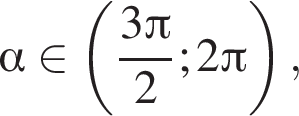 то
то 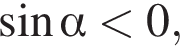 тогда по основному тригонометрическому тождеству, имеем:
тогда по основному тригонометрическому тождеству, имеем: 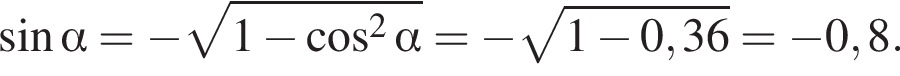
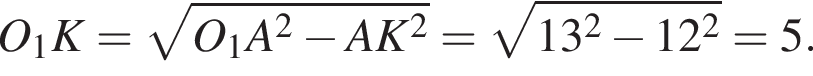
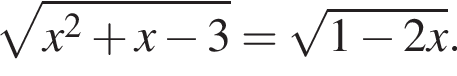
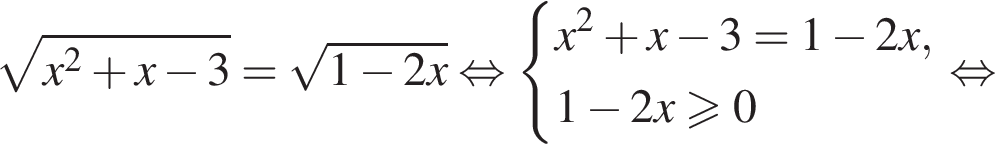
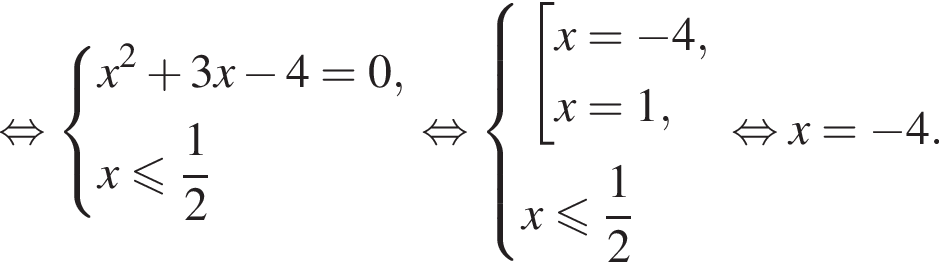
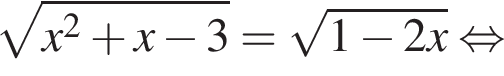
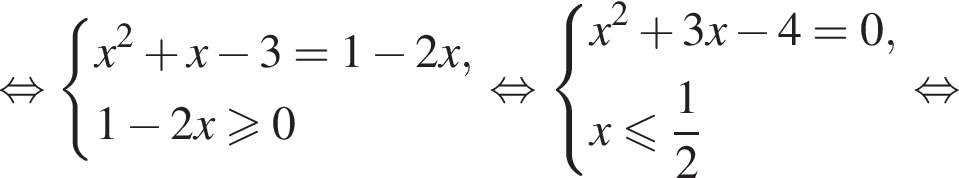
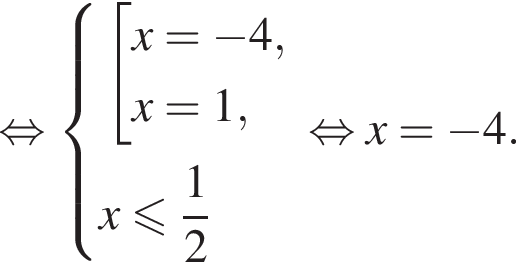
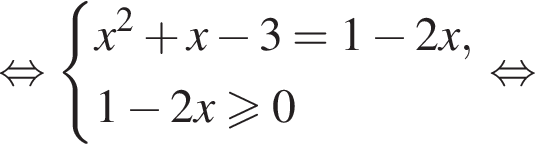
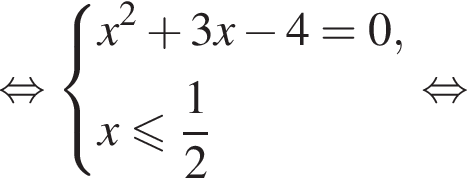
 если известно, что график функции проходит через точки
если известно, что график функции проходит через точки 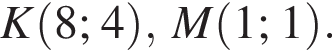 Постойте этот график.
Постойте этот график.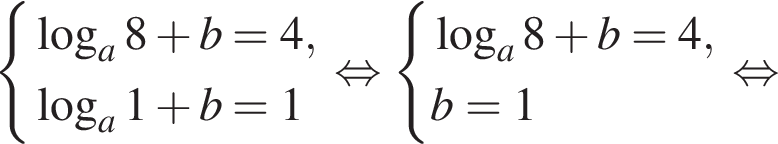
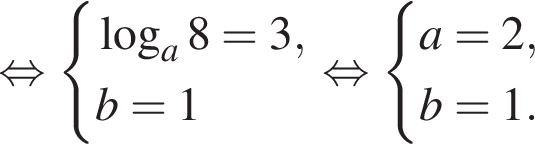
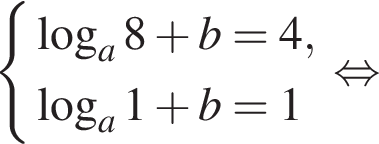
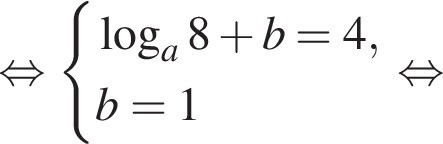
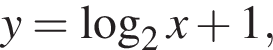 ее график получаем сдвигом графика
ее график получаем сдвигом графика 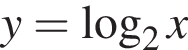 на одну единицу вверх (см. рис.).
на одну единицу вверх (см. рис.).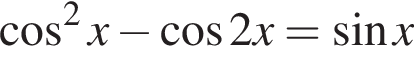 на промежутке от 10° до 200°.
на промежутке от 10° до 200°.
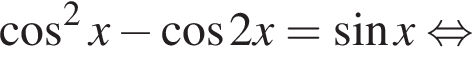
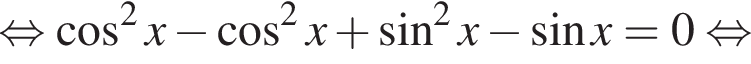
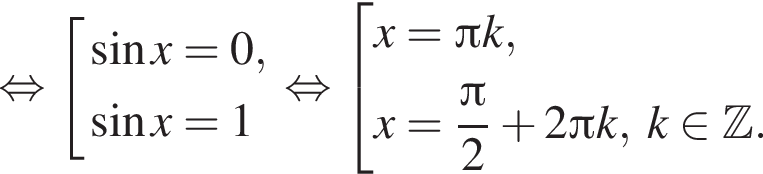
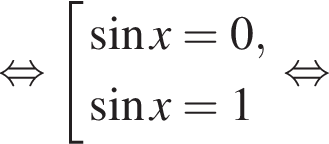
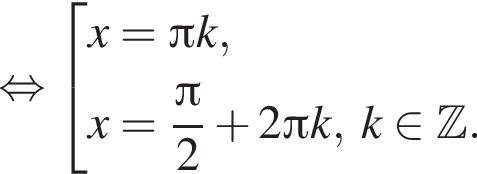
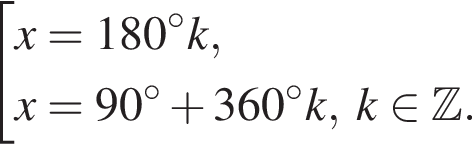
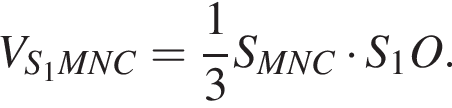 Площадь треугольника MNC равна
Площадь треугольника MNC равна 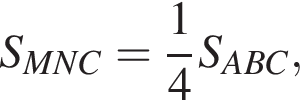 так как треугольник MNC подобен треугольнику ABC по трём углам, S1O = 2 · SO. Тогда
так как треугольник MNC подобен треугольнику ABC по трём углам, S1O = 2 · SO. Тогда