Заголовок:
Комментарий:
Готово, можно копировать.
РЕШУ ЦТ — математика–11Б
Вариант № 3432
1.  
i

Пло­щадь се­че­ния шара, про­хо­дя­ще­го через его центр, равна 9 Пи \см в квад­ра­те . Най­ди­те ра­ди­ус шара:

а)  9 см;

б)  3 см;

в)  18 см;

г)  27 см.

2.  
i

За­кон­чи­те фор­му­ли­ров­ку тео­ре­мы: «Пря­мая, пе­ре­се­ка­ю­щая одну из двух па­рал­лель­ных плос­ко­стей,...»

 

а)  па­рал­лель­на дру­гой плос­ко­сти

б)  при­над­ле­жит дру­гой плос­ко­сти

в)  пе­ре­се­ка­ет дру­гую плос­кость

г)  не пе­ре­се­ка­ет дру­гую плос­кость

3.  
i

Най­ди­те зна­че­ния вы­ра­же­ния 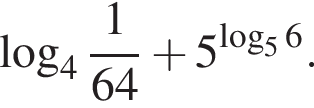ло­га­рифм по ос­но­ва­нию целая часть: 4, дроб­ная часть: чис­ли­тель: 1, зна­ме­на­тель: 64 плюс 5 в сте­пе­ни левая круг­лая скоб­ка ло­га­рифм по ос­но­ва­нию 5 6 пра­вая круг­лая скоб­ка .

4.  
i

Ре­ши­те урав­не­ние 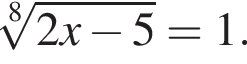ко­рень 8 сте­пе­ни из: на­ча­ло ар­гу­мен­та: 2x минус 5 конец ар­гу­мен­та = 1.

Со­кра­ти­те дробь: 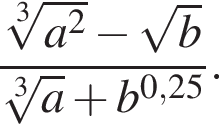{ дробь: чис­ли­тель: ко­рень 3 сте­пе­ни из: на­ча­ло ар­гу­мен­та: a в квад­ра­те конец ар­гу­мен­та минус ко­рень из: на­ча­ло ар­гу­мен­та: b конец ар­гу­мен­та , зна­ме­на­тель: ко­рень 3 сте­пе­ни из: на­ча­ло ар­гу­мен­та: a конец ар­гу­мен­та плюс b в сте­пе­ни левая круг­лая скоб­ка 0,25 пра­вая круг­лая скоб­ка конец дроби .

Диа­го­наль ос­но­ва­ния пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды равна 8 см, угол между плос­ко­стя­ми бо­ко­вой грани и ос­но­ва­ния равен 45°. Най­ди­те пло­щадь пол­ной по­верх­но­сти пи­ра­ми­ды.

7.  
i

Упро­сти­те вы­ра­же­ние: 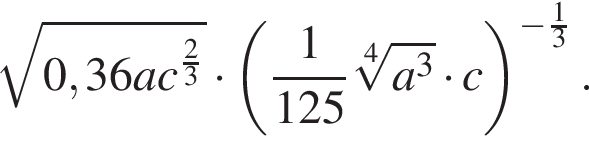ко­рень из: на­ча­ло ар­гу­мен­та: 0,36ac в сте­пе­ни левая круг­лая скоб­ка дробь: чис­ли­тель: 2, зна­ме­на­тель: 3 конец дроби конец ар­гу­мен­та пра­вая круг­лая скоб­ка умно­жить на левая круг­лая скоб­ка дробь: чис­ли­тель: 1, зна­ме­на­тель: 125 конец дроби ко­рень 4 сте­пе­ни из: на­ча­ло ар­гу­мен­та: a в кубе конец ар­гу­мен­та умно­жить на c пра­вая круг­лая скоб­ка в сте­пе­ни левая круг­лая скоб­ка минус дробь: чис­ли­тель: 1, зна­ме­на­тель: 3 конец дроби пра­вая круг­лая скоб­ка .

8.  
i

Ре­ши­те урав­не­ние: 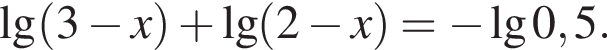\lg левая круг­лая скоб­ка 3 минус x пра­вая круг­лая скоб­ка плюс \lg левая круг­лая скоб­ка 2 минус x пра­вая круг­лая скоб­ка = минус \lg0,5.

9.  
i

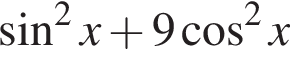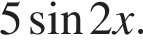
Най­ди­те все зна­че­ния пе­ре­мен­ной, при ко­то­рых равны зна­че­ния вы­ра­же­ний синус в квад­ра­те x плюс 9 ко­си­нус в квад­ра­те x и 5 синус 2 x.

10.  
i

Най­ди­те вы­со­ту H пра­виль­ной тре­уголь­ной пи­ра­ми­ды, у ко­то­рой бо­ко­вое ребро равно ребру ос­но­ва­ния, если объем пи­ра­ми­ды равен V. В от­ве­те за­пи­ши­те зна­че­ние ко­рень из: на­ча­ло ар­гу­мен­та: 3 конец ар­гу­мен­та H в кубе .