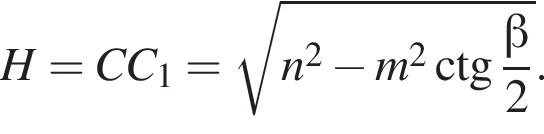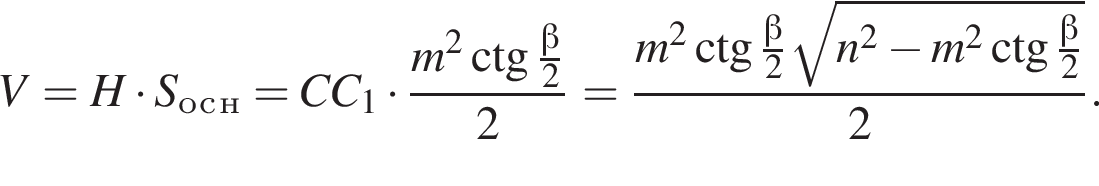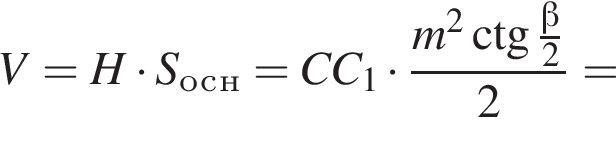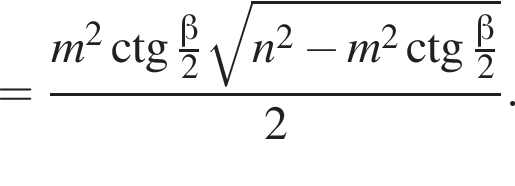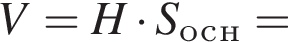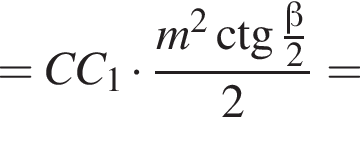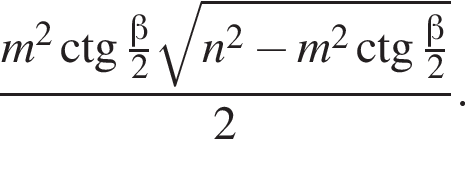1. Задание № 411 

Классификатор алгебры: 1.11. Действия с обратными тригонометрическими функциями
Задания на 1 балл
i
Значение выражения 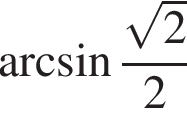 равно:
равно:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Решение. Согласно определению арксинуса 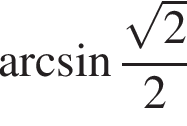 — число из отрезка
— число из отрезка 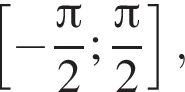 синус которого равен
синус которого равен ![]() Этим числом является
Этим числом является ![]()
Ответ: б).
Ответ: б).
411
б).
Классификатор алгебры: 1.11. Действия с обратными тригонометрическими функциями
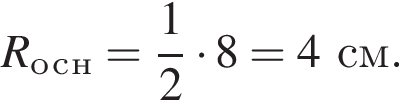
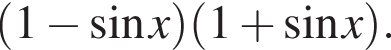
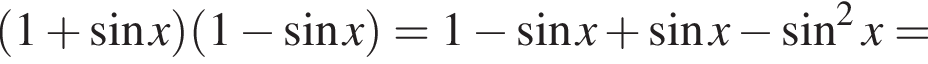
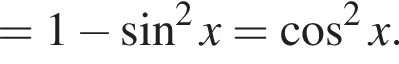
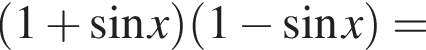
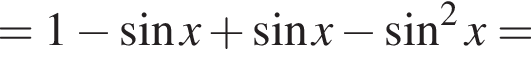


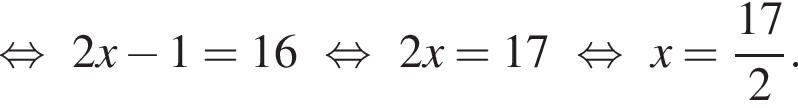
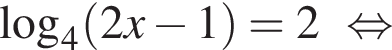
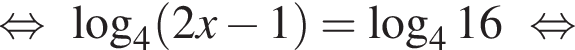
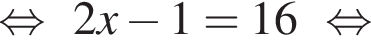
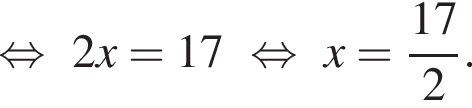
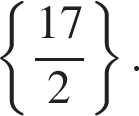
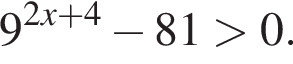
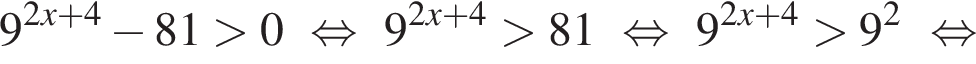



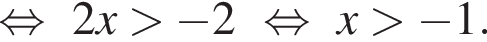
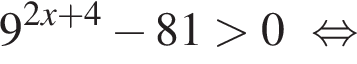
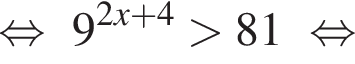
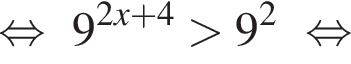
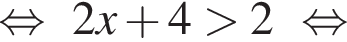

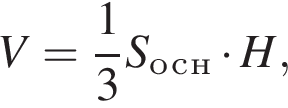 где H — высота пирамиды. Проведём
где H — высота пирамиды. Проведём  тогда треугольник AOM — прямоугольный и равнобедренный, так как
тогда треугольник AOM — прямоугольный и равнобедренный, так как 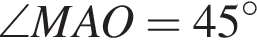 по условию, откуда, по теореме о сумме углов треугольника,
по условию, откуда, по теореме о сумме углов треугольника,  значит,
значит,  Так как O — центр описанной окружности, то
Так как O — центр описанной окружности, то 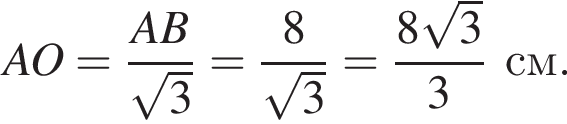 Таким образом,
Таким образом, 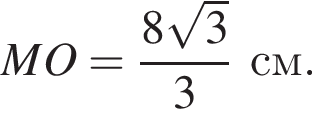
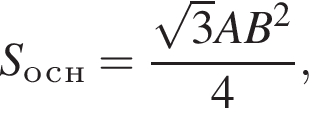 тогда получаем
тогда получаем 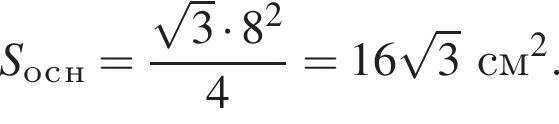
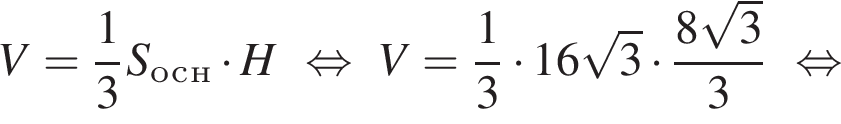
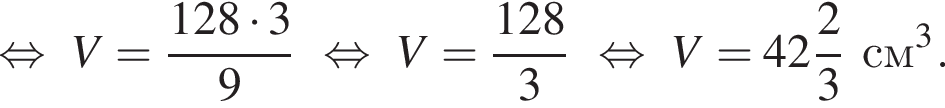
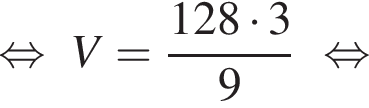
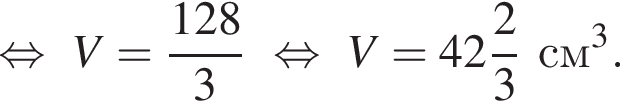
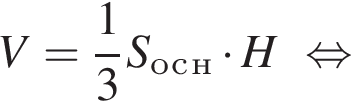
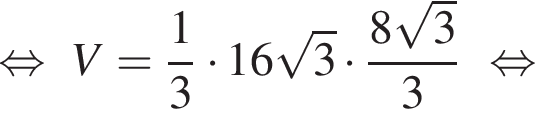
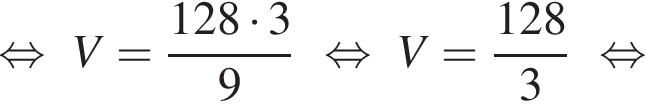
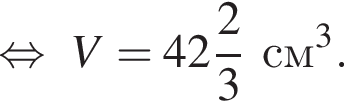
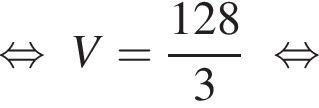
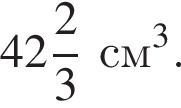
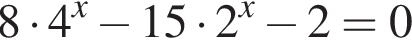
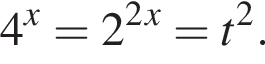 Решим вспомогательное уравнение:
Решим вспомогательное уравнение: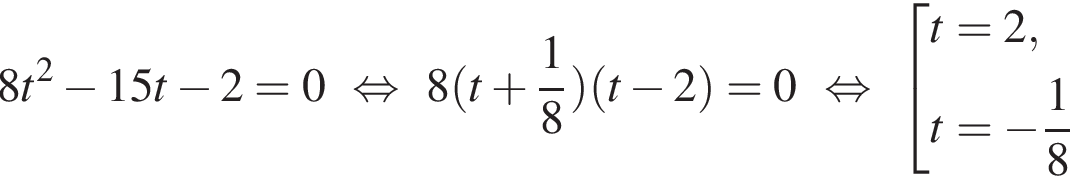
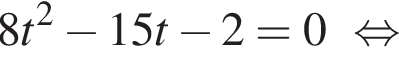
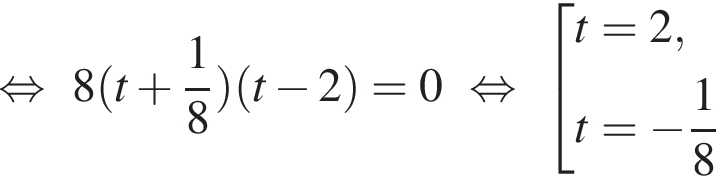
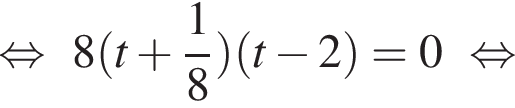
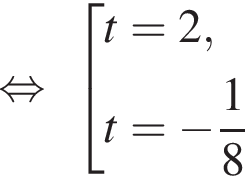
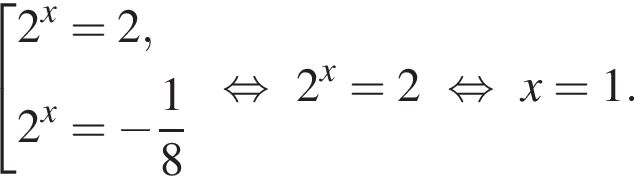
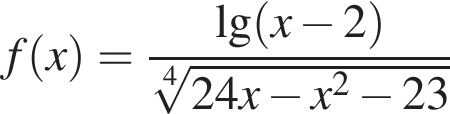 ?
?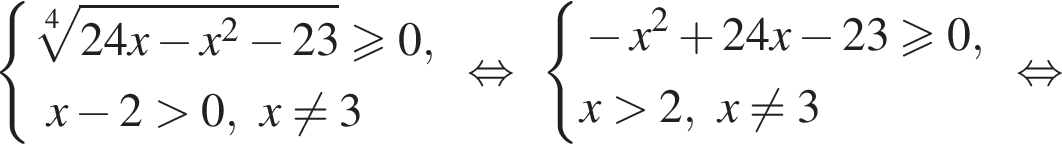
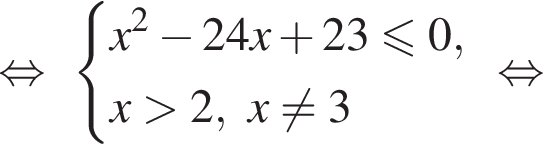
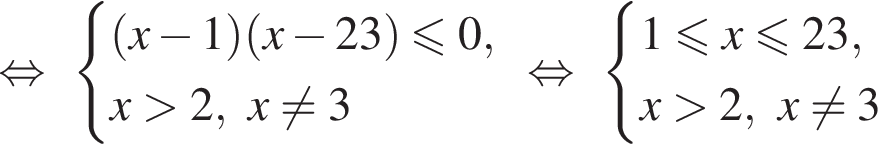
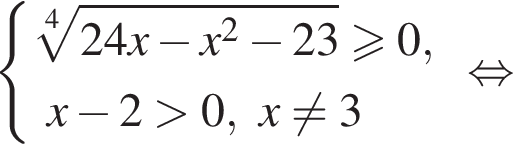
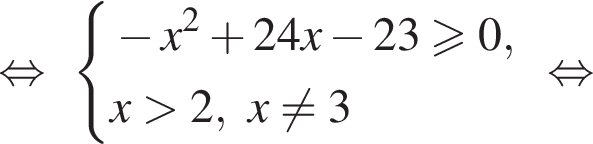
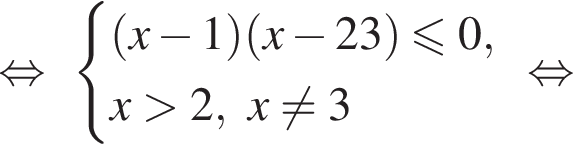
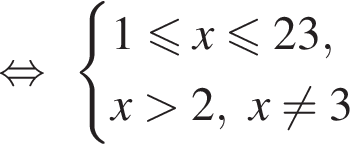
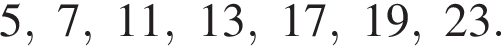
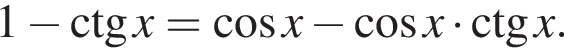
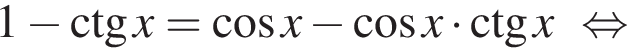

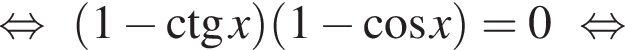
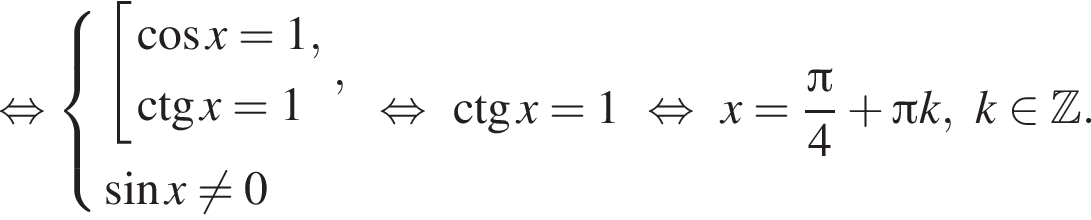
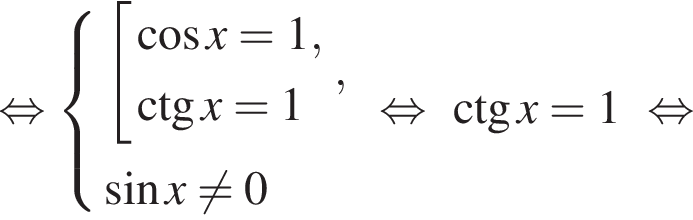
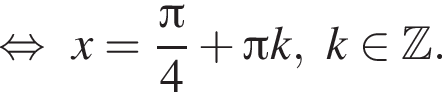
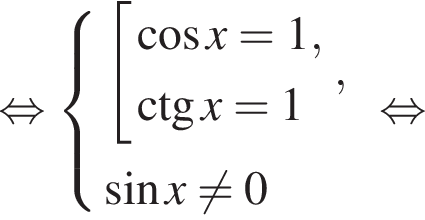
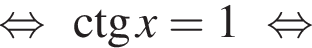
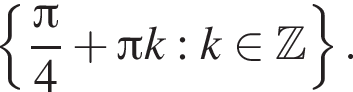
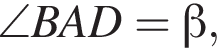 тогда
тогда 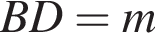 — меньшая диагональ. Если
— меньшая диагональ. Если 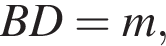 то
то 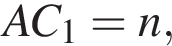 так как наибольшее расстояние между вершинами соответствует длине диагонали того диагонального сечения, которое проходит через большую диагональ основания.
так как наибольшее расстояние между вершинами соответствует длине диагонали того диагонального сечения, которое проходит через большую диагональ основания.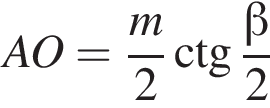 из прямоугольного треугольника AOB. Тогда:
из прямоугольного треугольника AOB. Тогда: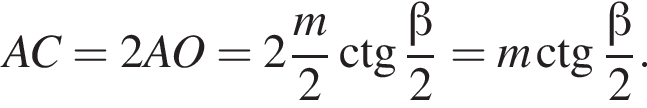
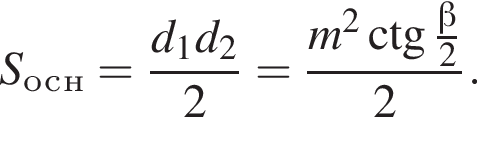 Высота параллелепипеда:
Высота параллелепипеда: