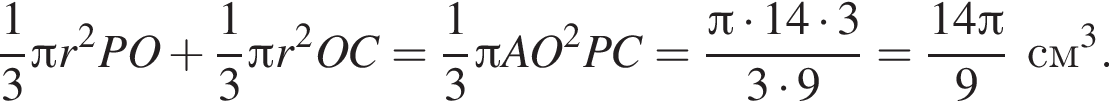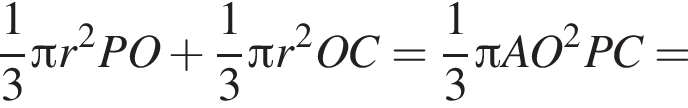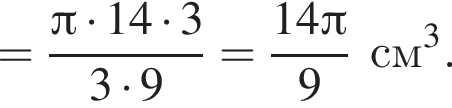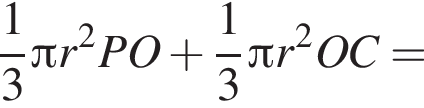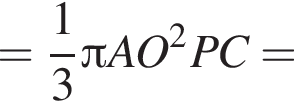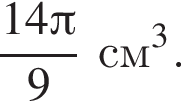Шар касается сторон треугольника ABC, у которого AB = 14, AC = 9 и BC = 13. Расстояние от центра O шара до плоскости ABC равно ![]() Найдите площадь поверхности шара.
Найдите площадь поверхности шара.
Решение. Пусть шар касается сторон BC, AB и AC в точках M, N, K соответственно. Проведем перпендикуляр OO1 к плоскости треугольника ABC. Радиусы OM, ON и OK перпендикулярны к сторонам треугольника. По теореме о трех перпендикулярах отрезки O1M, O1N, O1K перпендикулярны сторонам BC, AB и AC соответственно. Заметим, что прямоугольные треугольники OO1M, OO1N и OO1K равны по общему катету и гипотенузе, значит,
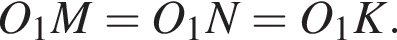 Поскольку точка O1 равноудалена от сторон треугольника ABC, то она является центром вписанной окружности.
Поскольку точка O1 равноудалена от сторон треугольника ABC, то она является центром вписанной окружности.
Найдем площадь треугольника ABC по формуле Герона:

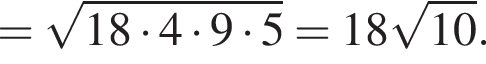
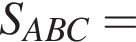
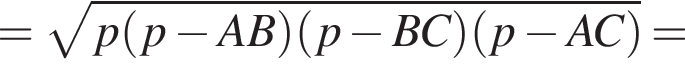
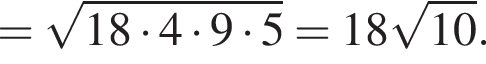

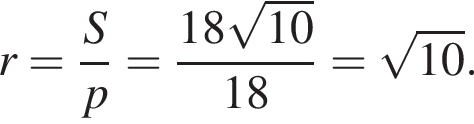
В прямоугольном треугольнике по теореме Пифагора найдем радиус шара, имеем:
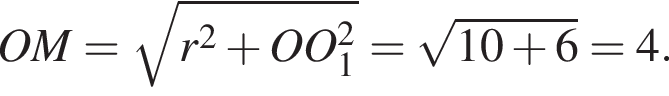
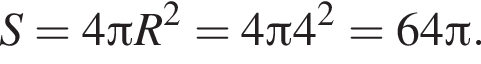
Ответ: 64π.
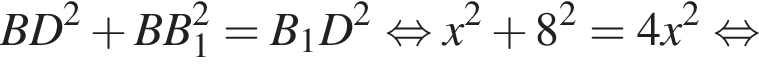
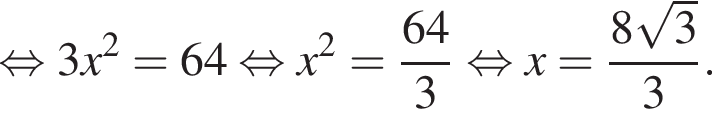
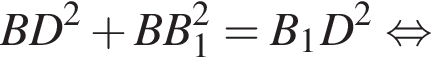
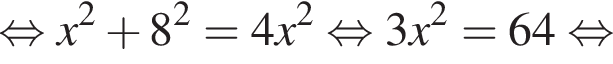
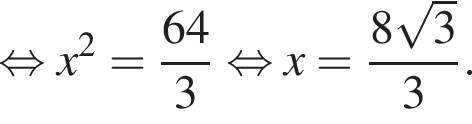
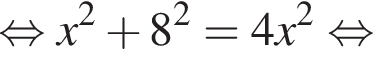
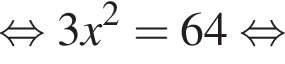
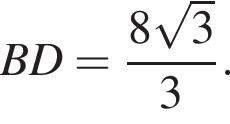 Найдем площадь треугольника AOB:
Найдем площадь треугольника AOB: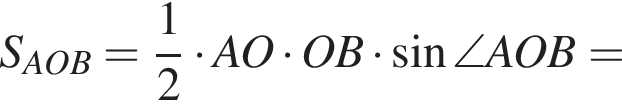
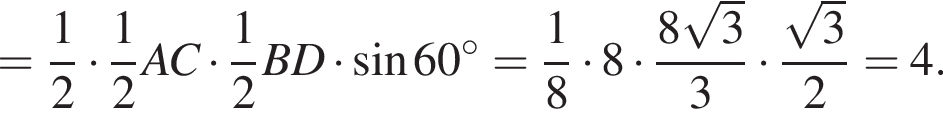
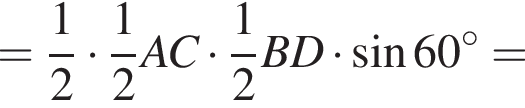
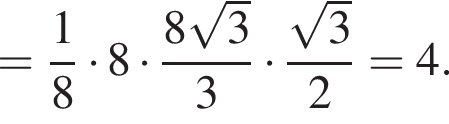

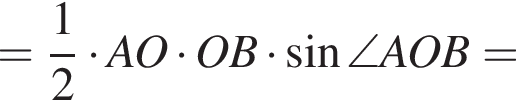
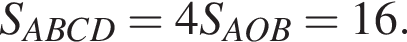 Найдем объем параллелепипеда:
Найдем объем параллелепипеда:
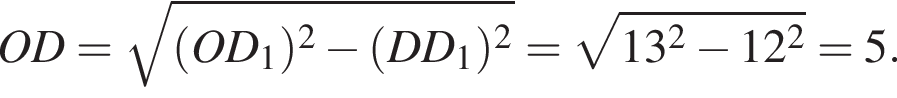
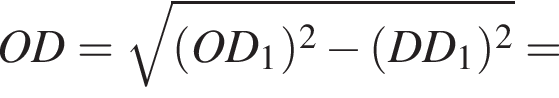
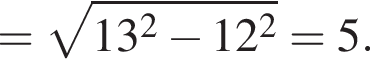
 то
то  Тогда
Тогда 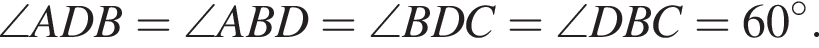


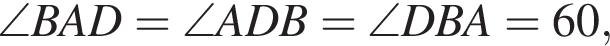

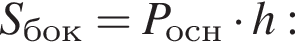

 следовательно, треугольник PBC — равносторонний, а значит, все грани правильной пирамиды PABC — равные равносторонние треугольники.
следовательно, треугольник PBC — равносторонний, а значит, все грани правильной пирамиды PABC — равные равносторонние треугольники. 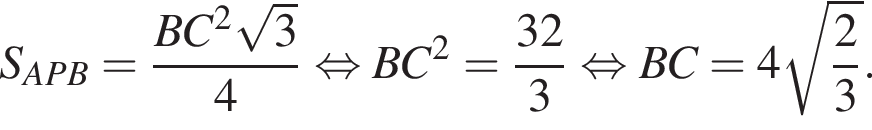
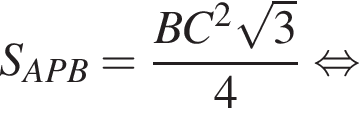
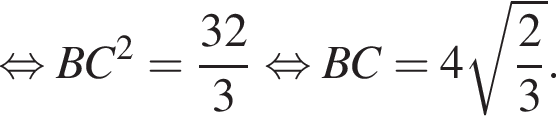
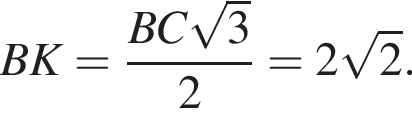 Поскольку соответственные элементы равных треугольников равны, поэтому высоты AK и BK равны, следовательно, треугольник AKB равнобедренный. Проведем медиану KM, которая также будет являться высотой. Найдем KM по теореме Пифагора:
Поскольку соответственные элементы равных треугольников равны, поэтому высоты AK и BK равны, следовательно, треугольник AKB равнобедренный. Проведем медиану KM, которая также будет являться высотой. Найдем KM по теореме Пифагора: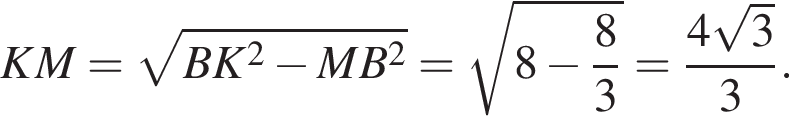
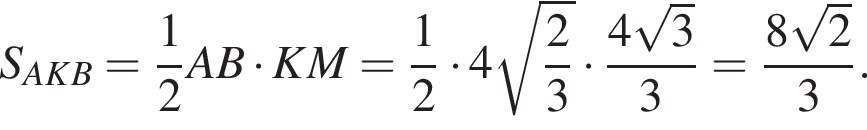
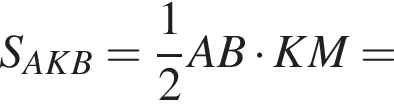
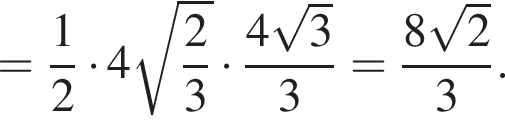
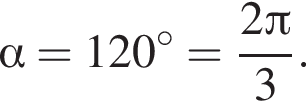 Найдем длину дуги сектора по формуле
Найдем длину дуги сектора по формуле 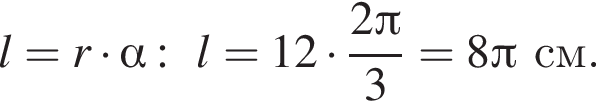
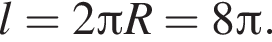 Тогда
Тогда 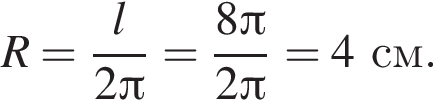
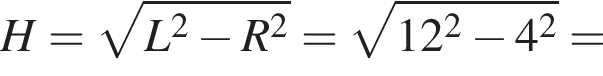

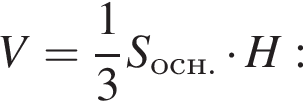
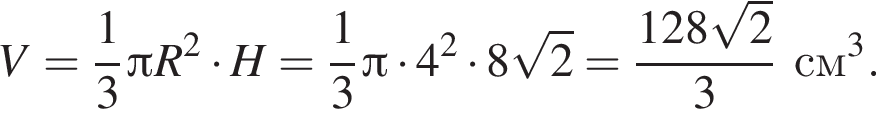
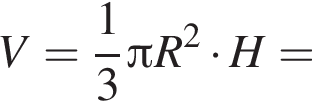
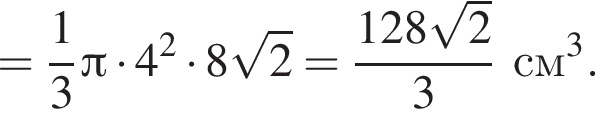
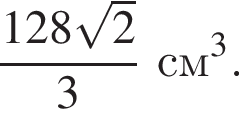
 найдем длину окружности основания:
найдем длину окружности основания: 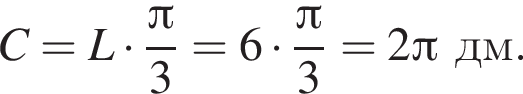
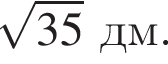 Тогда объем конуса равен
Тогда объем конуса равен 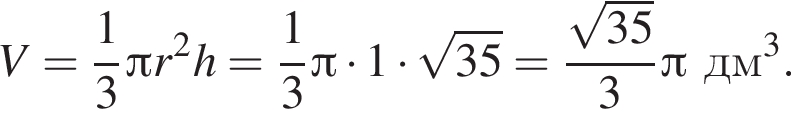
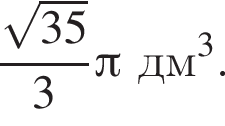
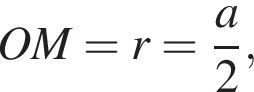 тогда SM — образующая конуса. Угол SMO = α — угол наклона образующей. Из равностороннего
тогда SM — образующая конуса. Угол SMO = α — угол наклона образующей. Из равностороннего 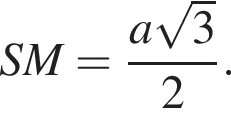 Тогда из треугольника SOM имеем:
Тогда из треугольника SOM имеем: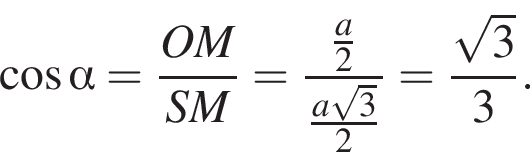
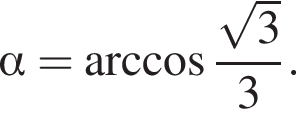 Тогда из треугольника SOM высота конуса
Тогда из треугольника SOM высота конуса 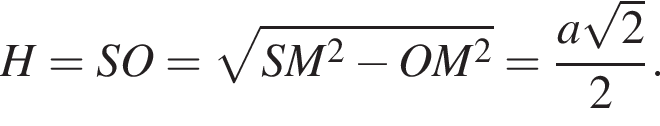
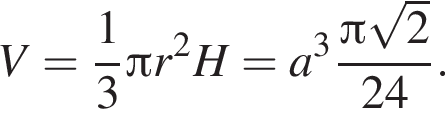
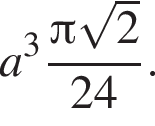
 Тогда из треугольника KOB
Тогда из треугольника KOB 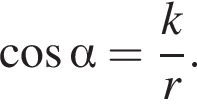 Так как угол α острый, получаем, что
Так как угол α острый, получаем, что 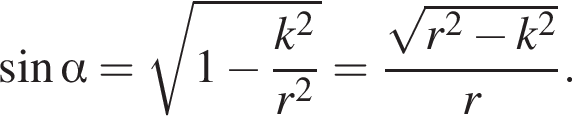
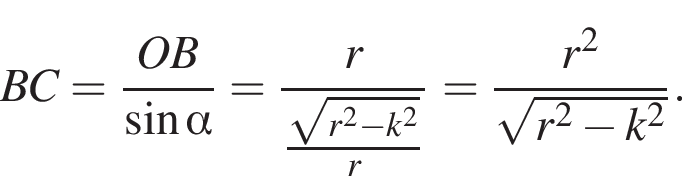
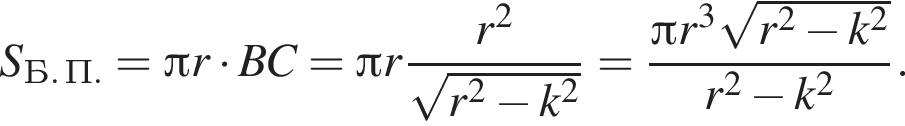

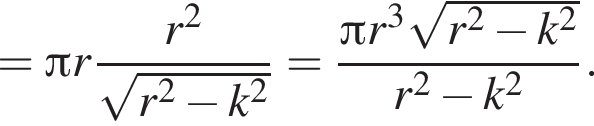
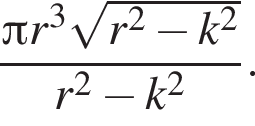
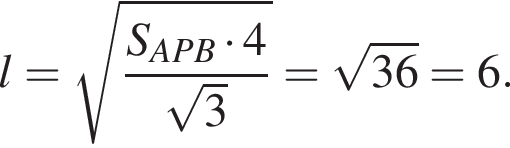
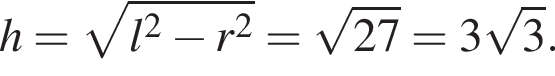
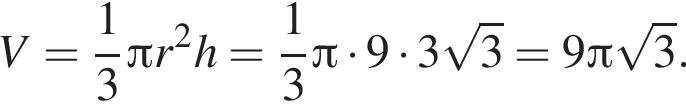
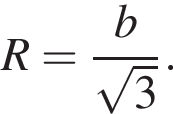 Из прямоугольного треугольника AOP:
Из прямоугольного треугольника AOP: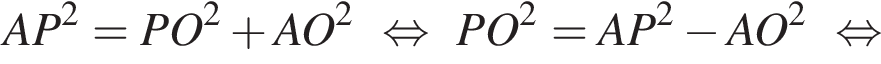
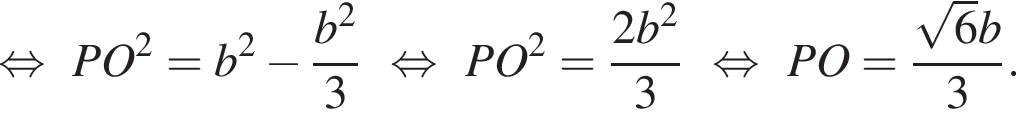
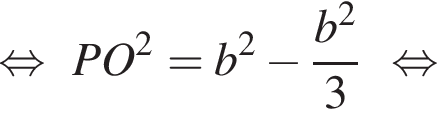
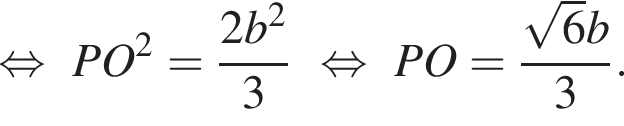
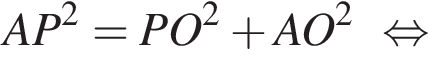
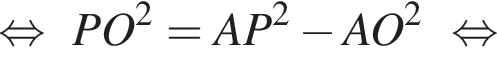
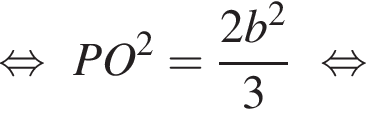
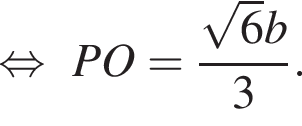

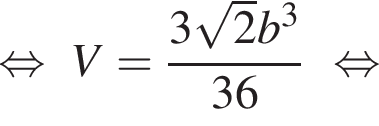
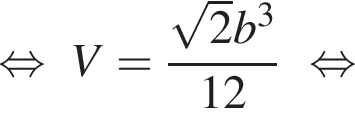
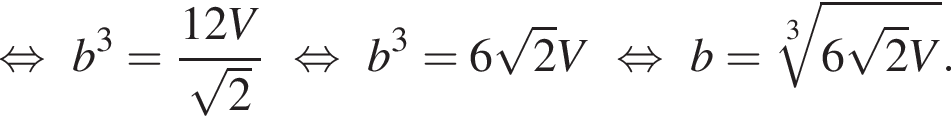
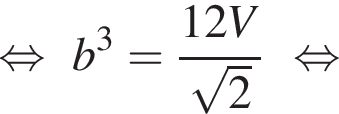
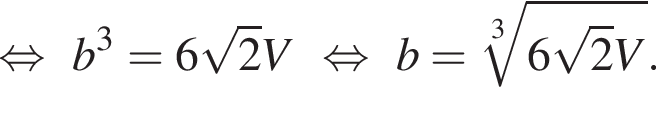
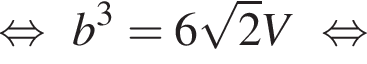
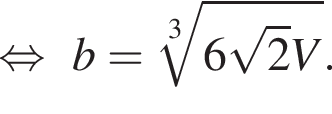
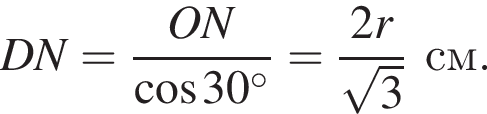
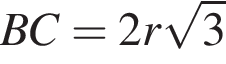 см.
см. см.
см.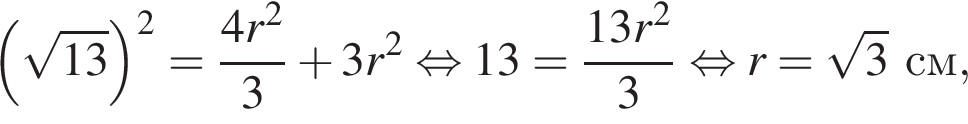
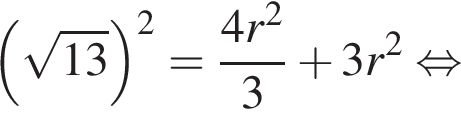
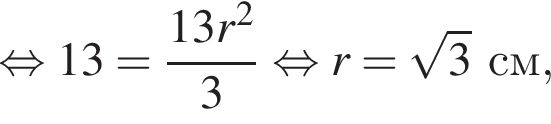
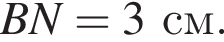 Следовательно, сторона основания равна
Следовательно, сторона основания равна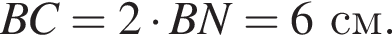
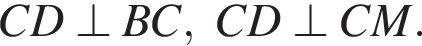 Так как плоскости сечений перпендикулярны, то
Так как плоскости сечений перпендикулярны, то  — линейный угол двугранного угла между ними. Значит,
— линейный угол двугранного угла между ними. Значит, 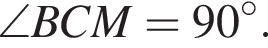
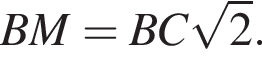
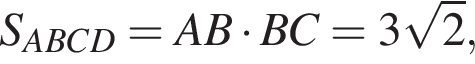 найдем площадь осевого сечения:
найдем площадь осевого сечения: 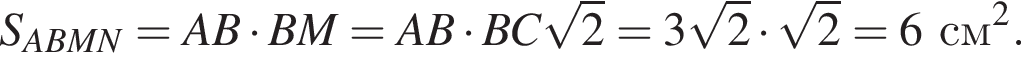
 площадь боковой поверхности
площадь боковой поверхности 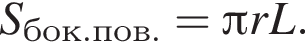 По условию:
По условию: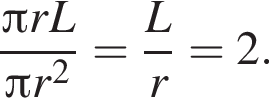
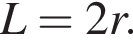 Высота конуса равна:
Высота конуса равна: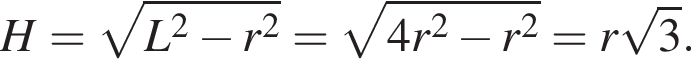
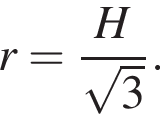 Воспользуемся формулой объема конуса:
Воспользуемся формулой объема конуса: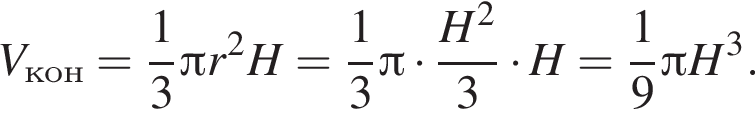
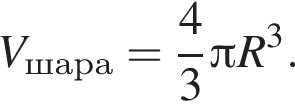
 тогда:
тогда: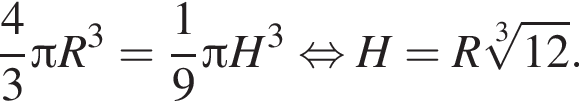
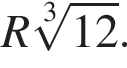
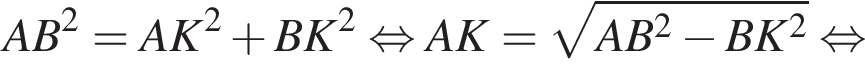
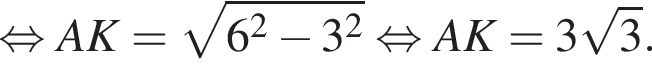
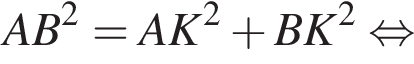


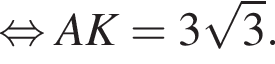
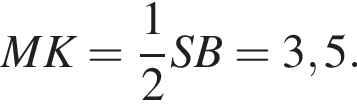 Применим теорему косинусов в треугольнике ASC:
Применим теорему косинусов в треугольнике ASC: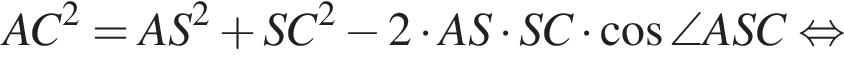
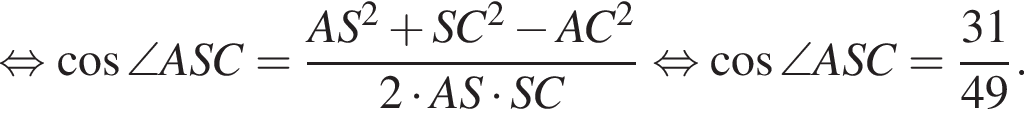
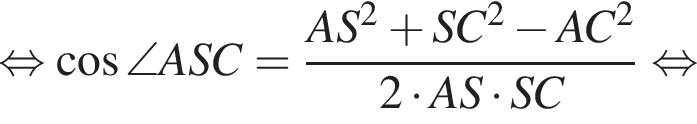
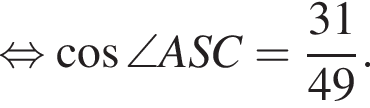
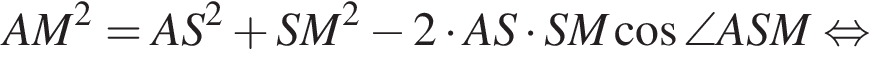
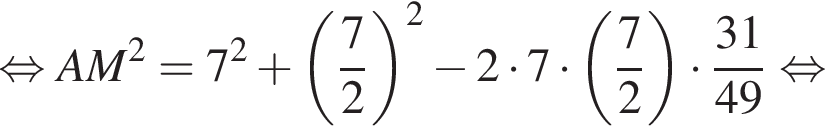
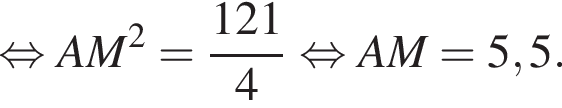
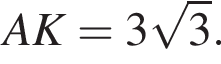 Наибольшей стороной является сторона AM, ее длина равна 5,5.
Наибольшей стороной является сторона AM, ее длина равна 5,5.
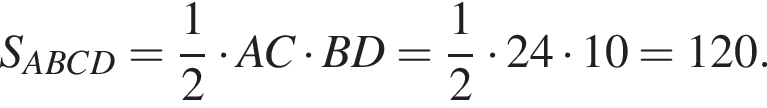
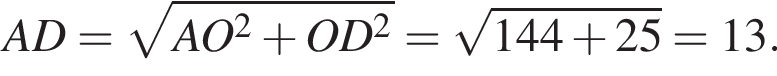
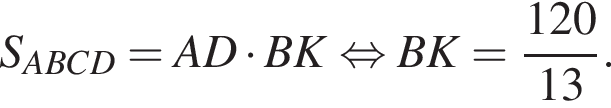
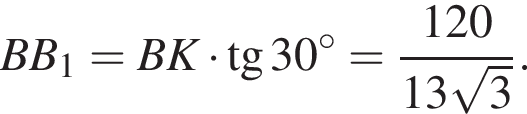
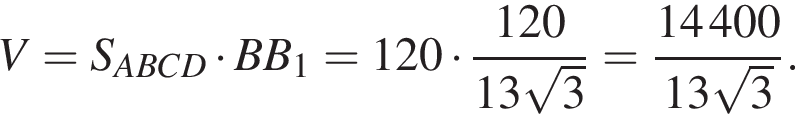
 равно
равно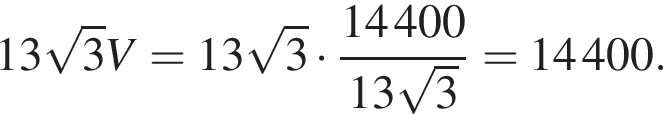

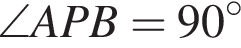 и
и  Найдите расстояние между точками P и C.
Найдите расстояние между точками P и C.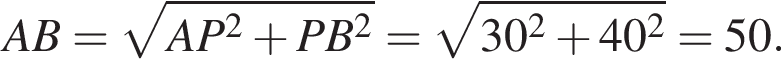
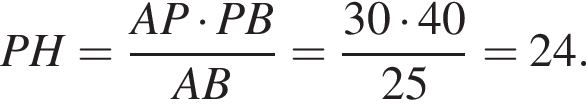
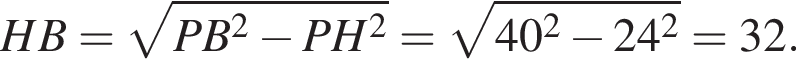
 и
и  Треугольник HCB — равносторонний, поскольку
Треугольник HCB — равносторонний, поскольку  и
и 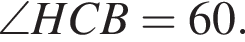 Тогда
Тогда 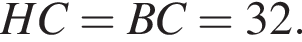
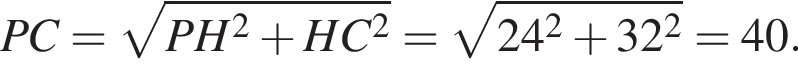
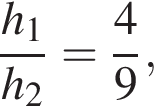 откуда
откуда 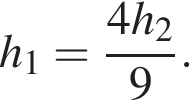 Так как цилиндры имеют равные объемы, имеем:
Так как цилиндры имеют равные объемы, имеем: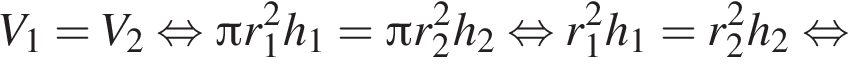
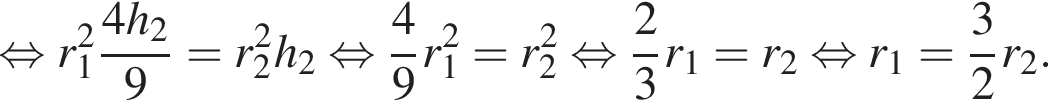
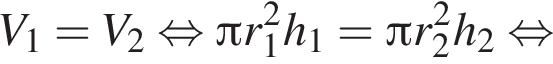
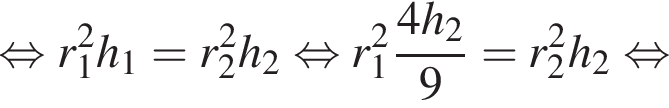

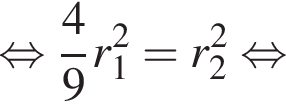
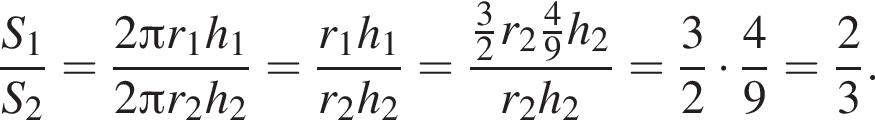
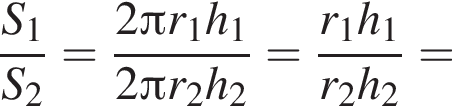
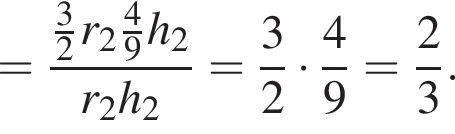
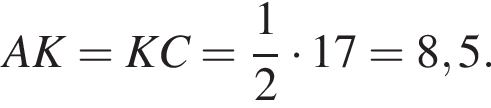 По теореме о сечении шара плоскостью отрезок OK перпендикулярен плоскости сечения, следовательно, треугольник KOC является прямоугольным. Тогда OC (радиус шара) равен
По теореме о сечении шара плоскостью отрезок OK перпендикулярен плоскости сечения, следовательно, треугольник KOC является прямоугольным. Тогда OC (радиус шара) равен 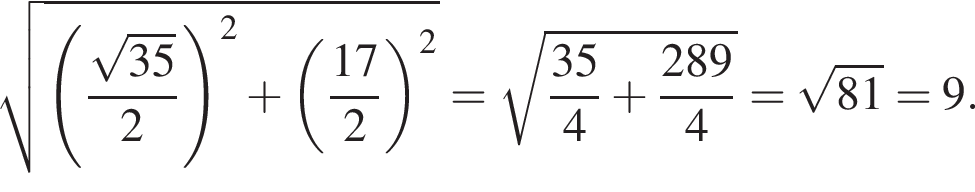
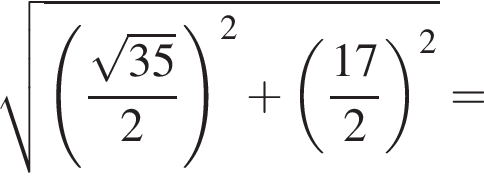
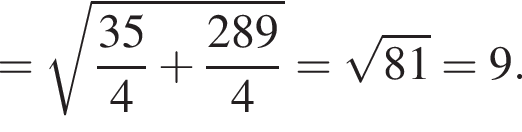
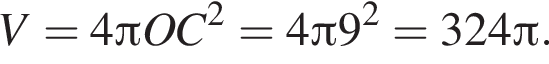
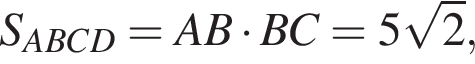 найдем площадь осевого сечения:
найдем площадь осевого сечения: 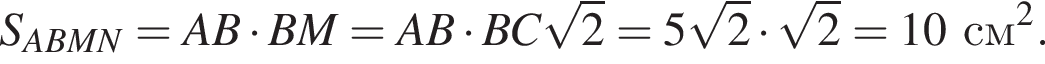
 Найдите объем пирамиды, если ее высота равна 2 см.
Найдите объем пирамиды, если ее высота равна 2 см.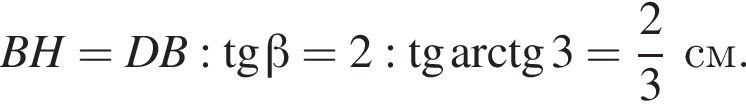
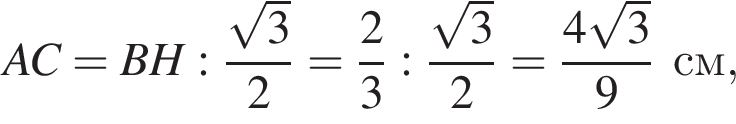
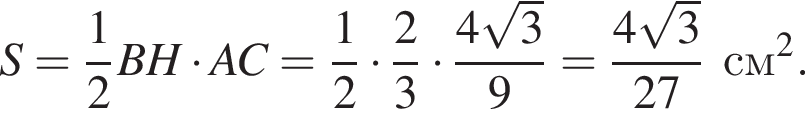
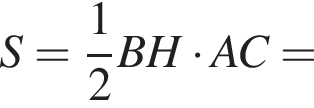
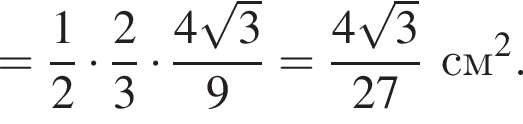
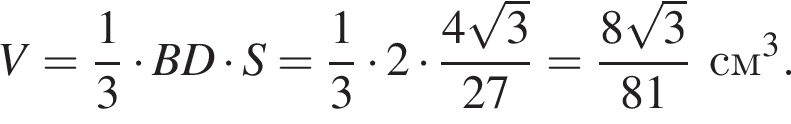
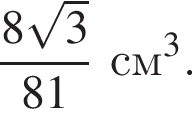
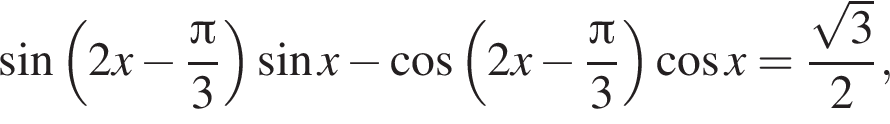
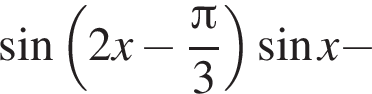
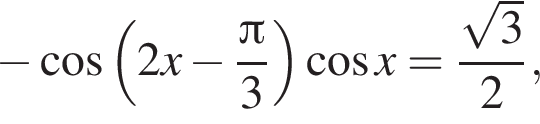
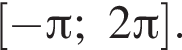
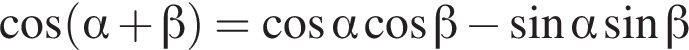 последовательно получаем:
последовательно получаем: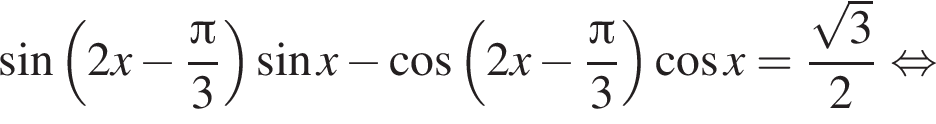
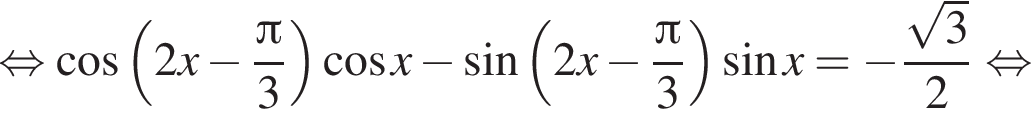
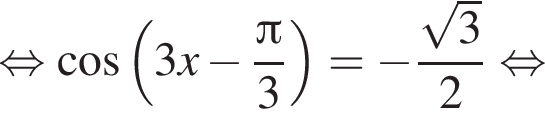
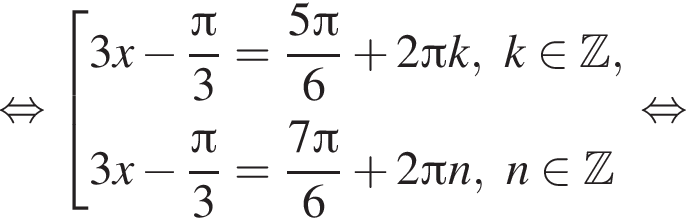
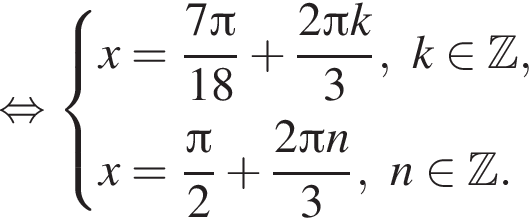
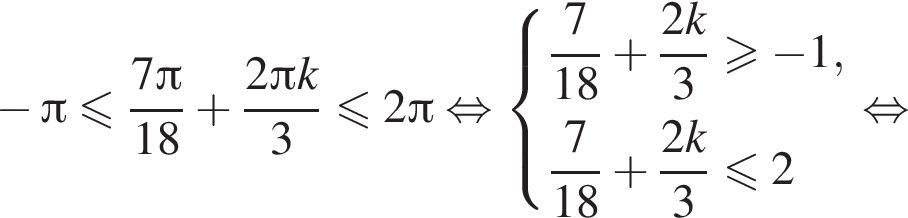
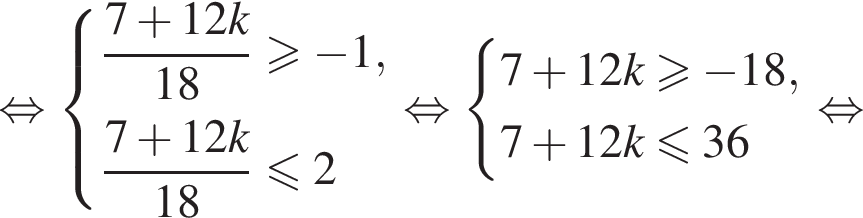
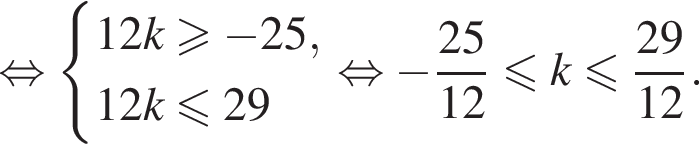
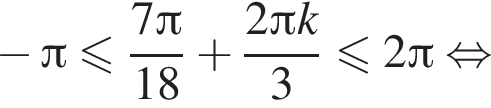
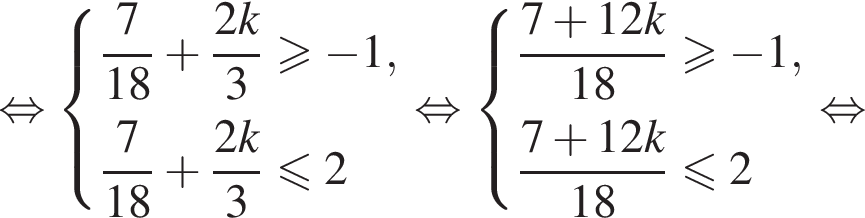
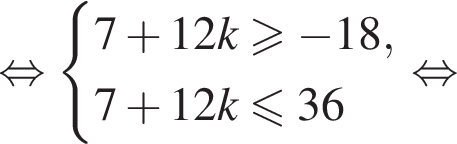
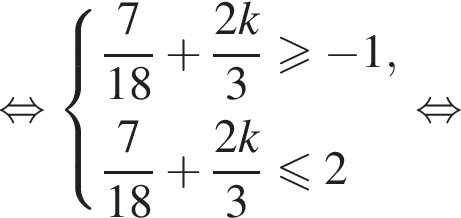
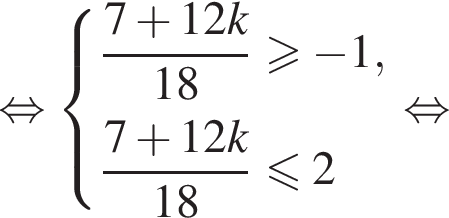
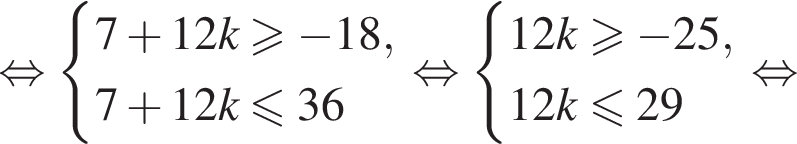
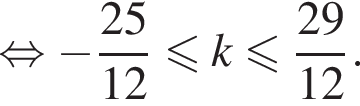
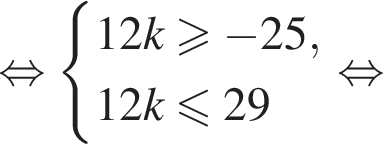
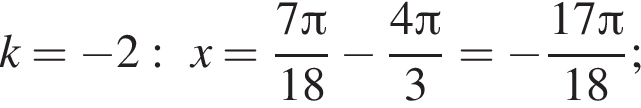
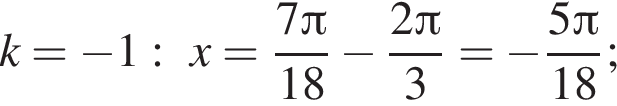
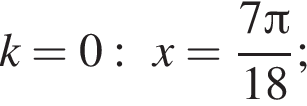
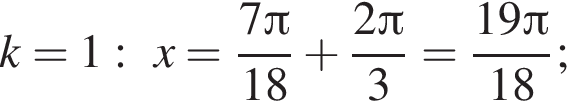
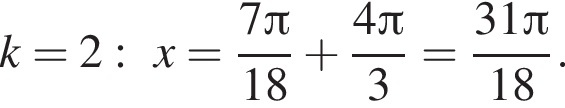
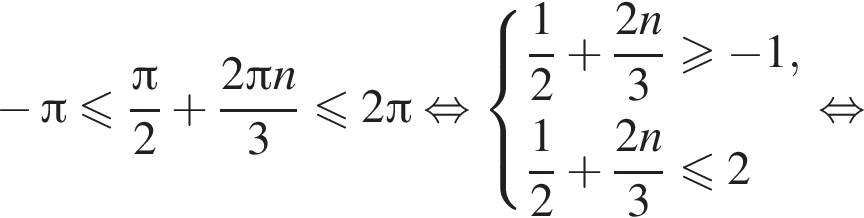

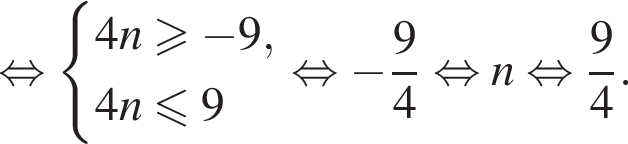
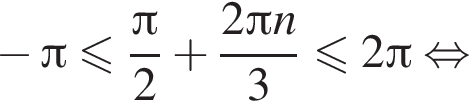
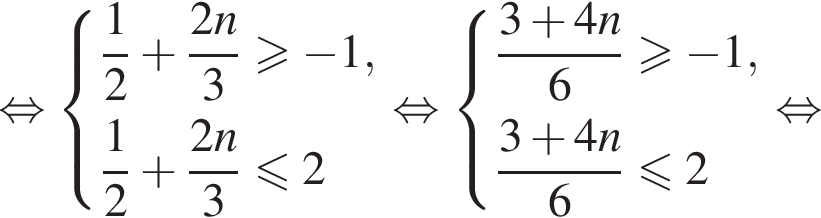
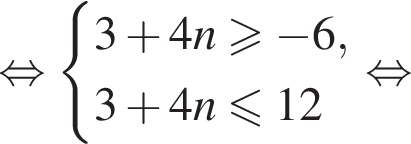
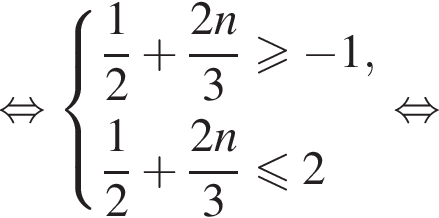
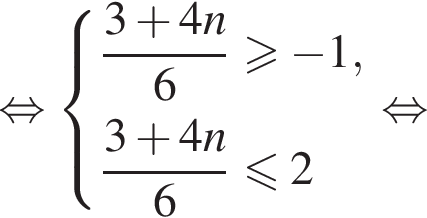
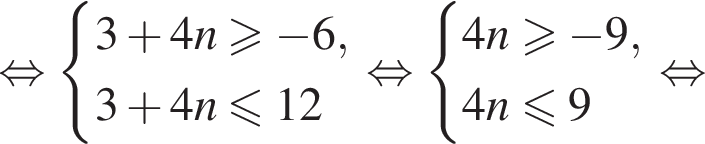
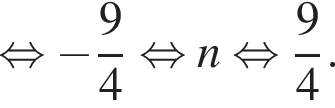
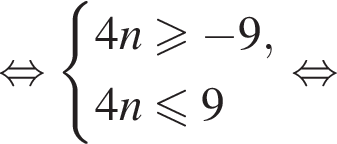
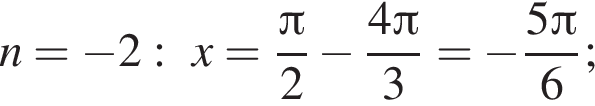
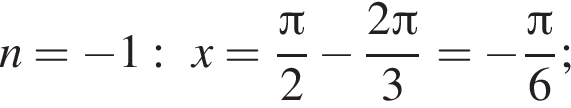
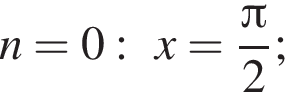
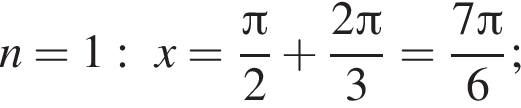
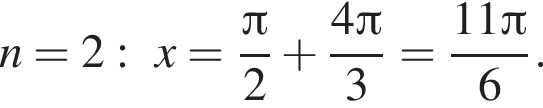
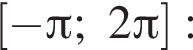
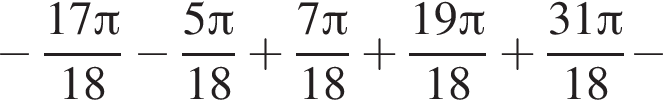
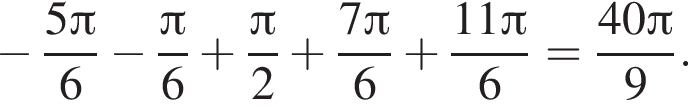
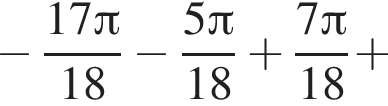
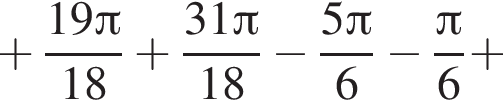
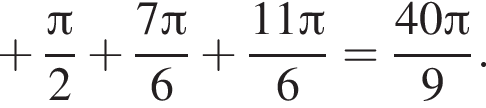
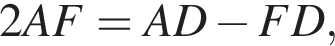 а так как
а так как  то
то  тогда по теореме Пифагора
тогда по теореме Пифагора 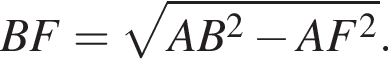 Подставим и получим, что
Подставим и получим, что 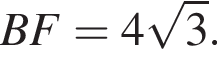 Радиус вписанной окружности равен
Радиус вписанной окружности равен 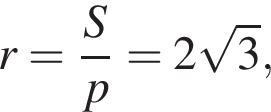 где p — полупериметр, а высота пирамиды равна
где p — полупериметр, а высота пирамиды равна 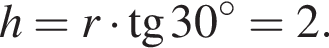 Тогда площадь трапеции равна
Тогда площадь трапеции равна 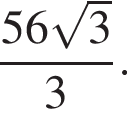
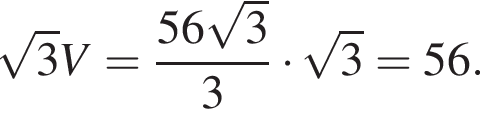
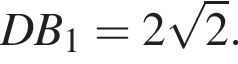 Диагональ BD квадрата ABCD равна 2, так как
Диагональ BD квадрата ABCD равна 2, так как 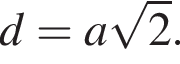 Найдём BB1 по теореме Пифагора:
Найдём BB1 по теореме Пифагора: 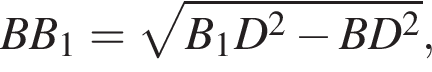 подставим и получим, что BB1 = 2, тогда объем призмы равен
подставим и получим, что BB1 = 2, тогда объем призмы равен 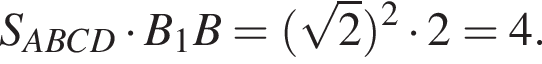
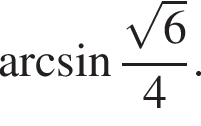 Найдите радиус R окружности, описанной около треугольника AKC. В ответе запишите значение выражения
Найдите радиус R окружности, описанной около треугольника AKC. В ответе запишите значение выражения 
 Поскольку прямая BL перпендикулярна прямой AC и прямой MK, то она перпендикулярна плоскости AKC. Значит, прямая KM — проекция прямой BB1 на плоскость AKC, следовательно, угол MKB — это угол между прямой BB1 и плоскостью сечения.
Поскольку прямая BL перпендикулярна прямой AC и прямой MK, то она перпендикулярна плоскости AKC. Значит, прямая KM — проекция прямой BB1 на плоскость AKC, следовательно, угол MKB — это угол между прямой BB1 и плоскостью сечения.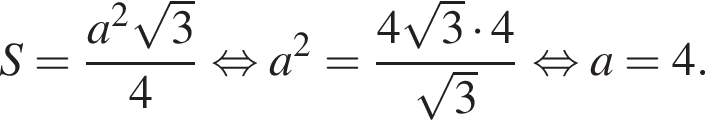
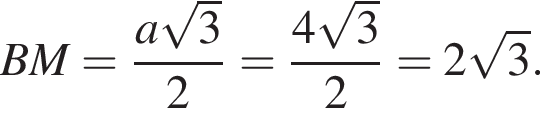
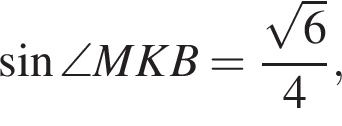 откуда
откуда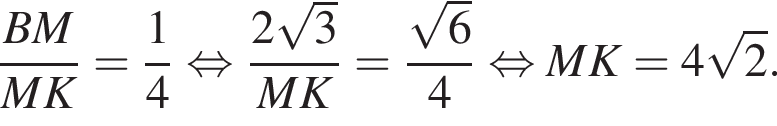
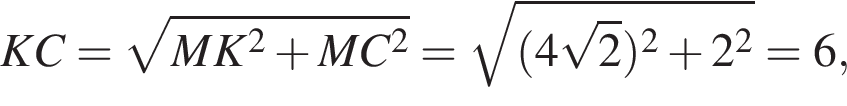

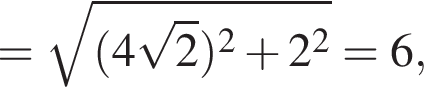
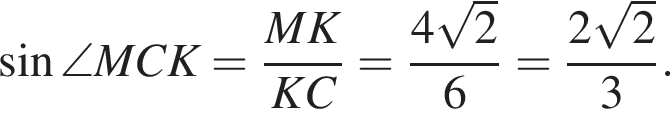
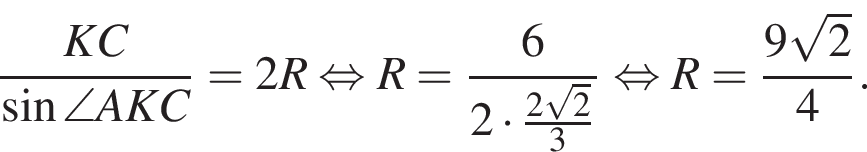
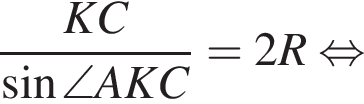
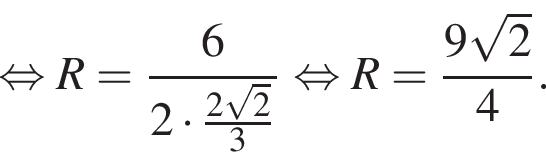
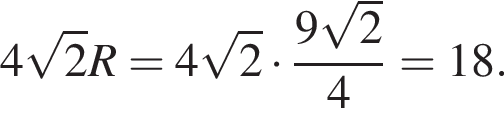
 По формуле длины дуги окружности
По формуле длины дуги окружности 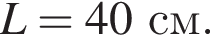 Треугольник POC прямоугольный, по теореме Пифагора
Треугольник POC прямоугольный, по теореме Пифагора 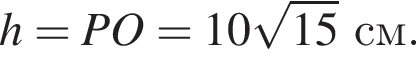
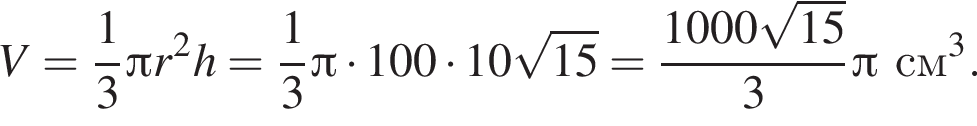
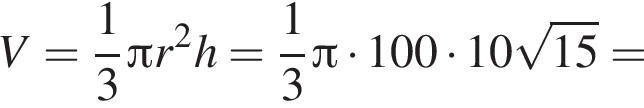
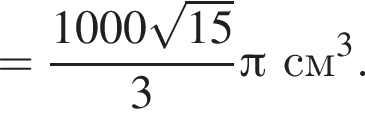
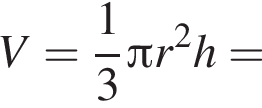
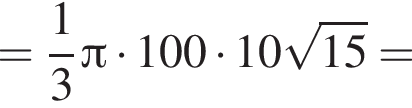
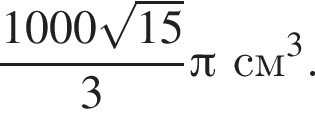
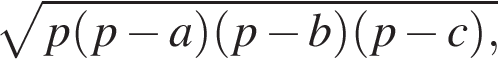 где p — полупериметр, в нашем случае
где p — полупериметр, в нашем случае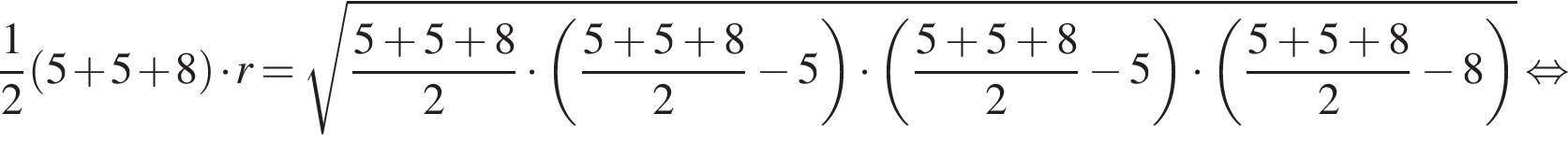
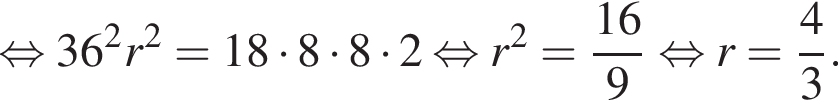
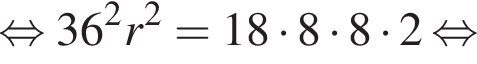
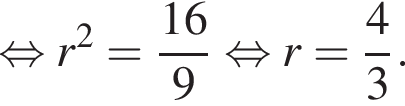
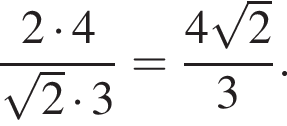 Площадь боковой поверхности равна половине произведения периметра основания на апофему. Имеем
Площадь боковой поверхности равна половине произведения периметра основания на апофему. Имеем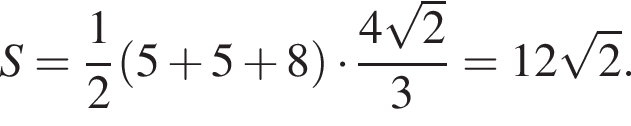
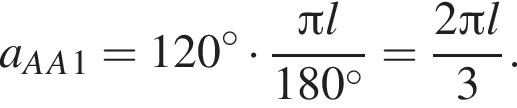
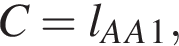 то
то 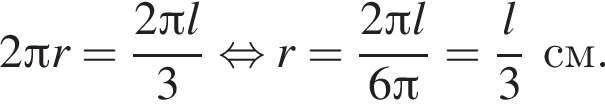
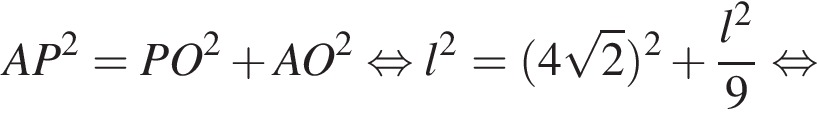
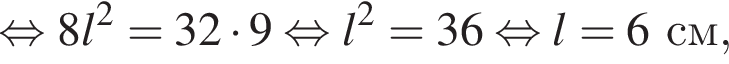
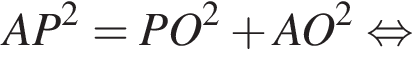
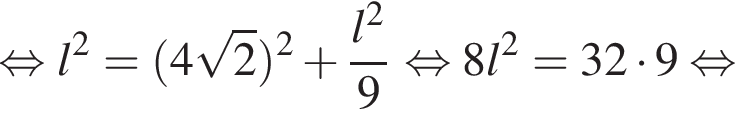

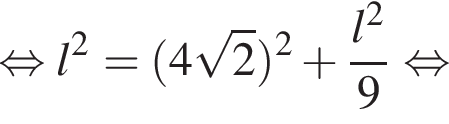

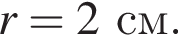
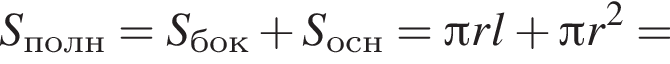
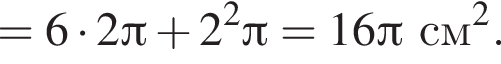

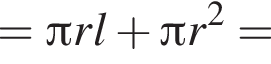
 , тогда
, тогда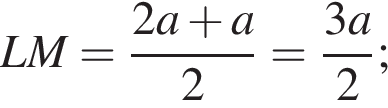
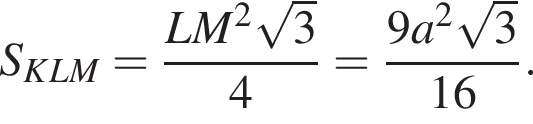
 см, угол AEA1 = 60°, тогда угол AA1E = 30°, тогда
см, угол AEA1 = 60°, тогда угол AA1E = 30°, тогда  см, а AA1 = 6 см.
см, а AA1 = 6 см.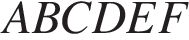 AE — меньшая диагональ,
AE — меньшая диагональ, 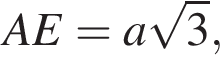 тогда
тогда 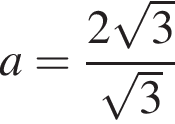 см.
см. см3; KK1 = AA1 = 6 см.
см3; KK1 = AA1 = 6 см.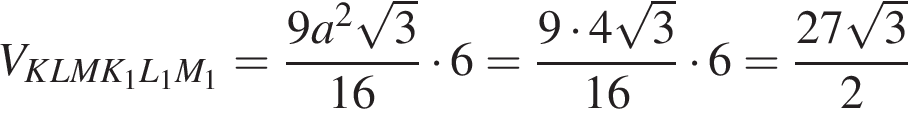
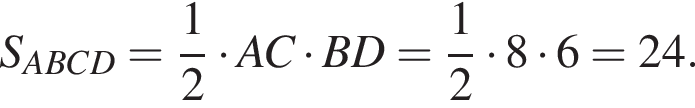

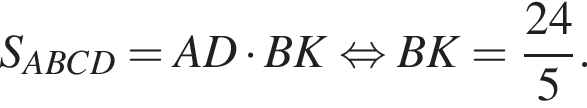
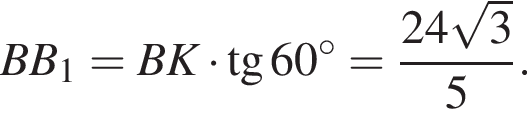
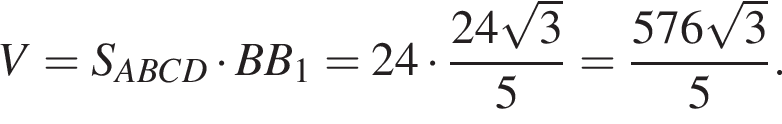
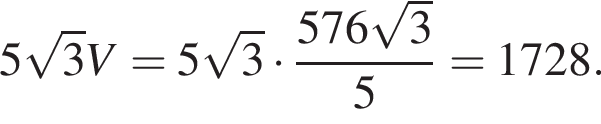
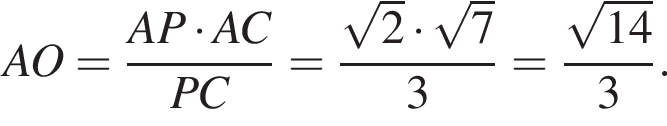 Объем этого тела равен:
Объем этого тела равен: